题目内容
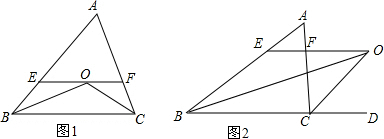
18.(1)如图1,在△ABC中BO、CO分别平分∠ABC、∠ACB,过点O作直线EF∥BC交AB于点E,交AC于点F,猜想EF和BE、CF有何关系?说明理由.(2)如图2,若将(1)中的“BO、CO分别平分∠ABC、∠ACB”改为“BO、CO分别平分∠ABC和∠ACB的外角”,其他条件不变,则EF与BE、CF的关系又如何?请说明理由.
分析 (1)等腰三角形有△BEO和△CFO,根据角平分线性质和平行线性质推出∠EBO=∠EOB,∠FOC=∠FCO,根据等角对等边推出即可;根据BE=OE,CF=OF即可得出EF与BE、CF之间的关系;
(2)等腰三角形有△BEO和△CFO,根据角平分线性质和平行线性质推出∠EBO=∠EOB,∠FOC=∠FCO,根据等角对等边推出即可;根据BE=OE,CF=OF即可得出EF与BE、CF之间的关系.
解答 解:(1)EF=BE+CF.
理由:∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=BE+CF.
(2)EF=BE-CF,
理由:∵BO平分∠ABC,CO平分∠ACD,
∴∠EBO=∠OBC,∠FCO=∠OCD,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCD,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=BE-CF.
点评 本题考查了角平分线定义,平行线的性质,等腰三角形的判定等知识点,关键是推出BE=OE,CF=OF.

练习册系列答案
相关题目
8.下列计算正确的是( )
| A. | a2+a3=a5 | B. | (a-b)2=a2-b2 | C. | a5÷a3=a2 | D. | (a2)3=a5 |