题目内容
12. 如图,AD是△ABC边BC上的高,CD=5,BD=3,cos∠BAD=tan∠ACD.
如图,AD是△ABC边BC上的高,CD=5,BD=3,cos∠BAD=tan∠ACD.(1)求证:AB=DC;
(2)求AC的长.
分析 (1)根据三角函数的定义,将cos∠BAD=tan∠ACD转化成用边表示,即可得出AB=DC;
(2)根据勾股定理得出AD的长,在Rt△ABC中,由勾股定理得AC的长.
解答 解:(1)∵AD是△ABC边BC上的高,
∴∠ADB=90°,
∵cos∠BAD=tan∠ACD,
∴$\frac{AD}{AB}$=$\frac{AD}{CD}$,
∴AB=CD;
(2)∵CD=5,BD=3,
∴AB=5,
∴AD=4,
在Rt△ABC中,AD2+CD2=AC2,
∴AC=$\sqrt{41}$.
点评 本题考查了解直角三角形的知识,勾股定理,注意熟练掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
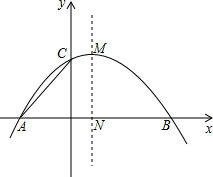 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点(点A位于点B的左侧),与y轴相交于点C,顶点M,对称轴MN与x轴相交于点N,连接AC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点(点A位于点B的左侧),与y轴相交于点C,顶点M,对称轴MN与x轴相交于点N,连接AC. 如图,在正方形ABCD中,E,F分别是AD、DC的中点,AF、BE交于点G,连接CG,试说明:△CGB是等腰三角形.
如图,在正方形ABCD中,E,F分别是AD、DC的中点,AF、BE交于点G,连接CG,试说明:△CGB是等腰三角形.