题目内容
北京某厂和上海某厂同时制成电子计算机若干台,北京厂可支援外地10台,上海厂可支援外地4台,现在决定给重庆8台,汉口6台.如果从北京运往汉口、重庆的运费分别是400元/台、800元/台,从上海运往汉口、重庆的运费分别是300元/台、500元/台.求:
(1)若总运费为8400元,上海运往汉口应是多少台?
(2)若要求总运费不超过8200元,共有几种调运方案?
(3)求出总运费最低的调运方案,最低总运费是多少元?
(1)若总运费为8400元,上海运往汉口应是多少台?
(2)若要求总运费不超过8200元,共有几种调运方案?
(3)求出总运费最低的调运方案,最低总运费是多少元?
考点:一次函数的应用
专题:
分析:(1)设出未知数,分别表示出北京、上海运往汉口、重庆的计算机台数,列出方程即可解决问题;
(2)结合(1),求出总运费y关于x的函数关系式,列出不等式即可解决问题;
(3)根据一次函数的性质即可解决问题.
(2)结合(1),求出总运费y关于x的函数关系式,列出不等式即可解决问题;
(3)根据一次函数的性质即可解决问题.
解答:解:(1)设上海运往汉口x台,则:
北京运往汉口6-x(台),北京运往重庆4+x(台),上海运往重庆4-x(台),
由题意得:300x+500(4-x)+400(6-x)+800(4+x)=8400,
解得:x=4(台).
(2)设上海运往汉口x台,
由(1)知:总费用y=300x+500(4-x)+400(6-x)+800(4+x)
=200x+7600;
∵y≤8200,即200x+7600≤8200,
∴x≤3,而x≥0,
∴x=0或1或2或3,
即共有4中调运方案.
(3)∵y=200x+7600,k=200>0,
∴y随x的增大而增大,
故当x=0时y取最小值,
此时y=7600.
北京运往汉口6-x(台),北京运往重庆4+x(台),上海运往重庆4-x(台),
由题意得:300x+500(4-x)+400(6-x)+800(4+x)=8400,
解得:x=4(台).
(2)设上海运往汉口x台,
由(1)知:总费用y=300x+500(4-x)+400(6-x)+800(4+x)
=200x+7600;
∵y≤8200,即200x+7600≤8200,
∴x≤3,而x≥0,
∴x=0或1或2或3,
即共有4中调运方案.
(3)∵y=200x+7600,k=200>0,
∴y随x的增大而增大,
故当x=0时y取最小值,
此时y=7600.
点评:该命题主要考查了一次函数在解决现实生活中调运问题方面的应用问题;解题的关键是准确把握题意,找准命题中隐含的数量关系,列出函数或方程来分析、判断或解答.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.
如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.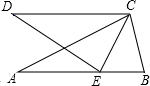 如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=
如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=