题目内容
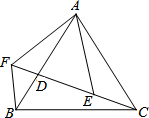 如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论:①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC,其中错误的是
如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论:①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC,其中错误的是考点:全等三角形的判定与性质
专题:
分析:根据题意结合图形证明△AFB≌△AEC;利用四点共圆及全等三角形的性质问题即可解决.
解答: 解:如图,
解:如图,
∵∠EAF=∠BAC,
∴∠BAF=∠CAE;
在△AFB与△AEC中,
,
∴△AFB≌△AEC(SAS),
∴BF=CE;∠ABF=∠ACE,
∴A、F、B、C四点共圆,
∴∠BFC=∠BAC=∠EAF;
故①、②、③正确,④错误.
故该题答案为④.
 解:如图,
解:如图,∵∠EAF=∠BAC,
∴∠BAF=∠CAE;
在△AFB与△AEC中,
|
∴△AFB≌△AEC(SAS),
∴BF=CE;∠ABF=∠ACE,
∴A、F、B、C四点共圆,
∴∠BFC=∠BAC=∠EAF;
故①、②、③正确,④错误.
故该题答案为④.
点评:该命题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是准确找出图形中隐含的全等三角形,灵活运用四点共圆等几何知识来分析、判断、推理或证明.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
下列各数中,3.14159,-
,0.131131113…,-π,
,-
,无理数的个数有( )
| 3 | 9 |
| 25 |
| 1 |
| 7 |
| A、1个 | B、2个 | C、3个 | D、4个 |
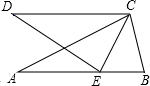 如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=
如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=