题目内容
8.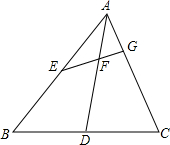 在△ABC中,D、E分别为BC、AB的中点,EG⊥AC于点G,EG、AD交于点F,若AG=4,BC=2$\sqrt{29}$,tan∠DAC=$\frac{1}{2}$,则AC=12.
在△ABC中,D、E分别为BC、AB的中点,EG⊥AC于点G,EG、AD交于点F,若AG=4,BC=2$\sqrt{29}$,tan∠DAC=$\frac{1}{2}$,则AC=12.
分析 设AC=2a,连接DE,过D作DH⊥AC于H,根据D、E分别为BC、AB的中点,于是得到DE=$\frac{1}{2}$AC=a,DE∥AC,CD=$\frac{1}{2}BC$=$\sqrt{29}$,根据已知条件tan∠DAC=$\frac{FG}{AG}=\frac{FG}{4}$=$\frac{1}{2}$,求得FG=2,通过△AGF∽△DFE,根据相似三角形的性质得到$\frac{AG}{DE}=\frac{FG}{EF}$,求得EF=$\frac{1}{2}$a,得到DH=EH=2+$\frac{1}{2}$a,HC=2a-4-a=a-4,根据勾股定理列方程$(\frac{1}{2}a+2)^{2}+(a-4)^{2}=29$,即可得到结论.
解答 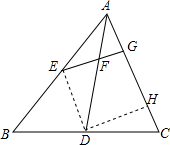 解:设AC=2a,连接DE,过D作DH⊥AC于H,
解:设AC=2a,连接DE,过D作DH⊥AC于H,
∵D、E分别为BC、AB的中点,
∴DE=$\frac{1}{2}$AC=a,DE∥AC,CD=$\frac{1}{2}BC$=$\sqrt{29}$,
∵tan∠DAC=$\frac{FG}{AG}=\frac{FG}{4}$=$\frac{1}{2}$,
∴FG=2,
∵DE∥AC,
∴△AGF∽△DFE,
∴$\frac{AG}{DE}=\frac{FG}{EF}$,
即$\frac{4}{a}=\frac{2}{EF}$,
∴EF=$\frac{1}{2}$a,
∴DH=EH=2+$\frac{1}{2}$a,HC=2a-4-a=a-4,
在Rt△DHC中,
DH2+CH2=DC2,
即$(\frac{1}{2}a+2)^{2}+(a-4)^{2}=29$,
解得:a=6,a=-$\frac{6}{5}$(舍去),
∴AC=12.
故答案为:12.
点评 本题考查了相似三角形的判定和性质,勾股定理,三角形的中位线的性质,正确的周长辅助线是解题的关键.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案| 有害污染物 | 排放量 | 占市区道路行驶机动车(含摩托车) 排放有害污染物总量 |
| 一氧化碳 | 11342吨 | 50% |
| 氮氧化物 | 2380吨 | |
| 非甲烷烃 | 2044吨 |
(1)根据上表填空:I、2000年南宁市区机动车(含摩托车)全年排放的有害污染物共3.2×104吨
(2)假设从2002年起,2年内南宁市的摩托车平均每年退役a万辆,同时增加公交车的数量,使新增公交车的运送能力总量等于退役的摩托车原有的运送能力总量.
①试找出增加公交车的数量y与时间n(年)之间的函数关系.
②若经过5年剩余的摩托车与新增公交车排放污染物的总量等于32万辆摩托车排放污染物总量的34%.求a的值.
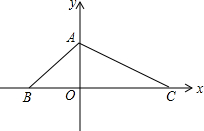 如图,已知,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12.
如图,已知,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12.