题目内容
15. 在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,
在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,(1)求CD的长;
(2)若AE是BC边上的中线,求△ABE的面积.
分析 (1)根据三角形的面积列出方程求解即可;
(2)根据三角形的面积公式即可得到结论.
解答 解:(1)∵CD是AB边上的高,
∴△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴CD=$\frac{AC•BC}{AB}$=$\frac{60}{13}$;
(2)∵△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×5×12=30cm2,
∵AE是BC边上的中线,
∴△ABE的面积=$\frac{1}{2}$S△ABC=15cm2.
点评 本题考查了三角形的面积,主要是直角三角形的面积的求法,是基础题.

练习册系列答案
相关题目
6.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过13小时的节气是( )
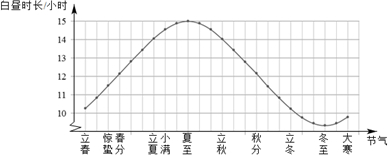

| A. | 惊蛰 | B. | 小满 | C. | 秋分 | D. | 大寒 |
7. 如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.AB=8cm,∠D=40°,那么AM的值和∠C的度数分别是( )
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.AB=8cm,∠D=40°,那么AM的值和∠C的度数分别是( )
 如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.AB=8cm,∠D=40°,那么AM的值和∠C的度数分别是( )
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.AB=8cm,∠D=40°,那么AM的值和∠C的度数分别是( )| A. | 3cm和30° | B. | 3cm和40° | C. | 4cm和50° | D. | 4cm和60° |
 如图,在△ABC中,∠C=90°,AC=BC=4cm,AD是∠BAC的平分线,DE⊥AB于E,那么△DBE的周长等于4$\sqrt{2}$cm.
如图,在△ABC中,∠C=90°,AC=BC=4cm,AD是∠BAC的平分线,DE⊥AB于E,那么△DBE的周长等于4$\sqrt{2}$cm.
 分别过P点画出AC的平行线和BC的垂线.
分别过P点画出AC的平行线和BC的垂线.