题目内容
11.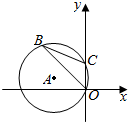 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 作直径CD,根据勾股定理求出OD,根据正切的定义求出tan∠CDO,根据圆周角定理得到∠OBC=∠CDO,等量代换即可.
解答 解: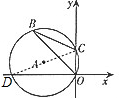 作直径CD,
作直径CD,
在Rt△OCD中,CD=6,OC=2,
则OD=$\sqrt{C{D}^{2}-O{C}^{2}}$=4$\sqrt{2}$,
tan∠CDO=$\frac{OC}{OD}$=$\frac{\sqrt{2}}{4}$,
由圆周角定理得,∠OBC=∠CDO,
则tan∠OBC=$\frac{\sqrt{2}}{4}$,
故选:C.
点评 本题考查的是圆周角定理、锐角三角函数的定义,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
1.小昱和阿帆均从同一本书的第1页开始,逐页依顺序在每一页上写一个数.小昱在第1页写1,且之后每一页写的数均为他在前一页写的数加2;阿帆在第1页写1,且之后每一页写的数均为他在前一页写的数加7.若小昱在某页写的数为101,则阿帆在该页写的数为何?( )
| A. | 350 | B. | 351 | C. | 356 | D. | 358 |
19.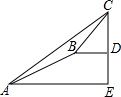 某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
 某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )| A. | 8.1米 | B. | 17.2米 | C. | 19.7米 | D. | 25.5米 |
16. 如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
 如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
 二次函数y=ax2+bx+c的图象如图,反比例函数y=$\frac{a}{x}$与正比例函数y=bx在同一坐标系内的大致图象是( )
二次函数y=ax2+bx+c的图象如图,反比例函数y=$\frac{a}{x}$与正比例函数y=bx在同一坐标系内的大致图象是( )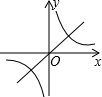


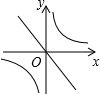
 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2). (2)
(2)
 x2+bx+c
x2+bx+c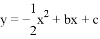 与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).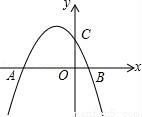
 得( )
得( )