题目内容
⊙O1与⊙O2相交于AB两点,⊙O1的半径为4厘米,⊙O2的半径为2厘米,AB=2厘米,求两圆的圆心距.
考点:圆与圆的位置关系
专题:
分析:如图,连接AO1,AO2,由勾股定理可以分别求出O1P和O2P,就可以求出结论.
解答: 解:连接AO1,AO2,由题意可知AO1=4,AO2=2.
解:连接AO1,AO2,由题意可知AO1=4,AO2=2.
∵AB=2,
∴AP=1,∠APO1=∠APO2=90°.
在Rt△APO1和Rt△APO2中,由勾股定理,得
PO1=
=
,PO2=
=
,
图1中,O1O2=PO1+PO2=
+
.
图2中,O1O2=PO1-PO2=
-
.
 解:连接AO1,AO2,由题意可知AO1=4,AO2=2.
解:连接AO1,AO2,由题意可知AO1=4,AO2=2.∵AB=2,
∴AP=1,∠APO1=∠APO2=90°.
在Rt△APO1和Rt△APO2中,由勾股定理,得
PO1=
| 42-12 |
| 15 |
| 22-12 |
| 3 |
图1中,O1O2=PO1+PO2=
| 15 |
| 3 |
图2中,O1O2=PO1-PO2=
| 15 |
| 3 |
点评:本题考查了勾股定理的运用,圆与圆的位置关系,解答时灵活作出辅助线运用勾股定理是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知ab=cd≠0,那么下列各式中错误的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以对角线OB1为一边作正方形OB1B2C1,则B2的坐标是
如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以对角线OB1为一边作正方形OB1B2C1,则B2的坐标是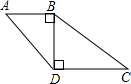 如图所示,已知∠ABD=∠BDC=90°,AB=6,sinA=
如图所示,已知∠ABD=∠BDC=90°,AB=6,sinA=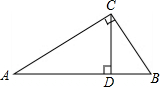 如图,∠ACB=90°,CD⊥AB,求证:△ACD∽△CBD∽ABC.
如图,∠ACB=90°,CD⊥AB,求证:△ACD∽△CBD∽ABC.