题目内容
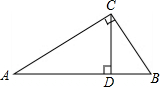如图，∠ACB=90°，CD⊥AB，求证：△ACD∽△CBD∽ABC．考点：相似三角形的判定
专题：证明题
分析：求出∠CDA=∠ACB=90°，根据有两个角对应相等的两三角形相似得出△ACD∽△ABC，△CBD∽△ABC，即可得出答案．
解答：证明：∵∠ACB=90°，CD⊥AB，
∴∠CDA=∠ACB=90°，
∵∠A=∠A，
∴△ACD∽△ABC，
同理△CBD∽△ABC，
∴△ACD∽△CBD∽ABC．
∴∠CDA=∠ACB=90°，
∵∠A=∠A，
∴△ACD∽△ABC，
同理△CBD∽△ABC，
∴△ACD∽△CBD∽ABC．
点评：本题考查了相似三角形的判定定理的应用，注意：①有两个角对应相等的两三角形相似．
练习册系列答案
相关题目