题目内容
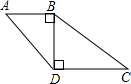如图所示，已知∠ABD=∠BDC=90°，AB=6，sinA=| 4 |
| 5 |
考点：解直角三角形
专题：
分析：先在Rt△ABD中，由sinA=
=
，设BD=4x，则AD=5x，根据勾股定理得出（4x）2+62=（5x）2，解方程求出x的值，求出BD，然后在Rt△BCD中利用勾股定理求出BC，再根据锐角三角函数的定义即可求出sinC的值．
| BD |
| AD |
| 4 |
| 5 |
解答：解：设BD=4x，则AD=5x，
在Rt△ABD中，根据勾股定理得
（4x）2+62=（5x）2，
解得x=±2（负值舍去），
所以BD=8．
在Rt△BCD中，∵∠BDC=90°，BD=8，CD=12，
∴BC=
=
=4
，
∴sinC=
=
=
．
在Rt△ABD中，根据勾股定理得
（4x）2+62=（5x）2，
解得x=±2（负值舍去），
所以BD=8．
在Rt△BCD中，∵∠BDC=90°，BD=8，CD=12，
∴BC=
| BD2+CD2 |
| 82+122 |
| 13 |
∴sinC=
| BD |
| BC |
| 8 | ||
4
|
2
| ||
| 13 |
点评：本题考查了解直角三角形，锐角三角函数的定义，勾股定理，难度适中．正确求出BD的值是解题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
如图，中间是一盏路灯，周围有一围栏杆，图（2）（3）表示的是这些栏杆的影子，但没有画完，请你把图（2）（3）补充完整．