题目内容
19．定义符号min{a，b}的含义为：当a＞b时min{a，b}=b；当a＜b时min{a，b}=a．如：min{1，3}=-3，min{-4，-2}=-4，则min{-x2+2，-x}的最大值是（ ）| A． | -1 | B． | -2 | C． | 1 | D． | 0 |
分析 先求出两个函数的交点坐标，再根据min的定义解答即可．
解答 解：联立$\left\{\begin{array}{l}{y=-{x}^{2}+2}\\{y=-x}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=1}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-2}\end{array}\right.$，
所以min{-x2+2，-x}的最大值是1．
故选：C．
点评 本题考查了二次函数的最值问题，读懂题目信息，理解定义符号的意义并考虑求两个函数的交点是解题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
10．
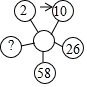如图，从左上角标注2的圆圈开始，顺时针方向按an+b的规律，（n表示前一个圆圈中的数字，a，b是常数）转换后得到下一个圆圈中的数，则标注“？”的圆圈中的数应是（ ）
如图，从左上角标注2的圆圈开始，顺时针方向按an+b的规律，（n表示前一个圆圈中的数字，a，b是常数）转换后得到下一个圆圈中的数，则标注“？”的圆圈中的数应是（ ）| A． | 119 | B． | 120 | C． | 121 | D． | 122 |
7．
如图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，则$\frac{GH}{EF}$的值是（ ）
如图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，则$\frac{GH}{EF}$的值是（ ）| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{2}$ |
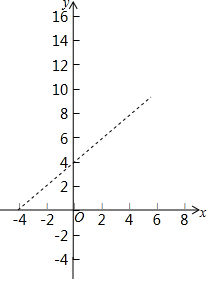如图，已知 A（-4，0），B（0，4），现以A点为位似中心，相似比为4：9，将OB向右侧放大，B点的对应点为C．
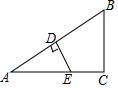如图，已知在△ABC中，∠C=90°，D是AB上一点，且BD=BC，过点D作DE⊥AB，交AC于E，若AC=4，BC=3，AB=5，则△ADE的周长等于6．
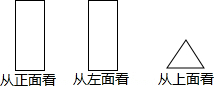已知某几何体从正面和左面看都是大小相同的长方形，从上面看是一个等边三角形，如图所示．