题目内容
5.(1)问题背景如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证:$\sqrt{2}$PA=PB+PC.
小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:
第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);
第二步:证明Q,B,P三点共线,进而原题得证.
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.
(3)拓展延伸
如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=$\frac{4}{3}$AC,AB⊥AC,垂足为A,则OC的最小值为$\frac{3}{2}$.
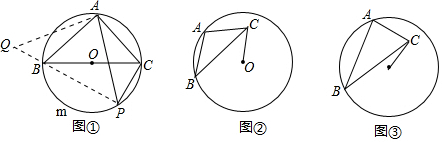
分析 (1)将△PAC绕着点A顺时针旋转90°至△QAB(如图①),只要证明△APQ是等腰直角三角形即可解决问题;
(2)如图②中,连接OA,将△OAC绕点O顺时针旋转90°至△QAB,连接OB,OQ,在△BOQ中,利用三边关系定理即可解决问题;
(3)如图③构造相似三角形即可解决问题.作AQ⊥OA,使得AQ=$\frac{4}{3}$OA,连接OQ,BQ,OB.由△QAB∽OAC,推出BQ=$\frac{4}{3}$OC,当BQ最小时,OC最小;
解答 (1)证明:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);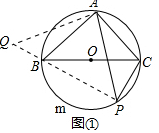
∵BC是直径,
∴∠BAC=90°,
∵AB=AC,
∴∠ACB=∠ABC=45°,
由旋转可得∠QBA=∠PCA,∠ACB=∠APB=45°,PC=QB,
∵∠PCA+∠PBA=180°,
∴∠QBA+∠PBA=180°,
∴Q,B,P三点共线,
∴∠QAB+∠BAP=∠BAP+∠PAC=90°,
∴QP2=AP2+AQ2=2AP2,
∴QP=$\sqrt{2}$AP=QB+BP=PC+PB,
∴$\sqrt{2}$AP=PC+PB.
(2)解:如图②中,连接OA,将△OAC绕点A顺时针旋转90°至△QAB,连接OB,OQ,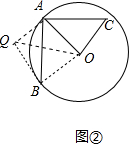
∵AB⊥AC
∴∠BAC=90°
由旋转可得 QB=OC,AQ=OA,∠QAB=∠OAC
∴∠QAB+∠BAO=∠BAO+∠OAC=90°
∴在Rt△OAQ中,OQ=3$\sqrt{2}$,AO=3
∴在△OQB中,BQ≥OQ-OB=3$\sqrt{2}$-3
即OC最小值是3$\sqrt{2}$-3
(3)如图③中,作AQ⊥OA,使得AQ=$\frac{4}{3}$OA,连接OQ,BQ,OB.
∵∠QAO=∠BAC=90°,
∠QAB=∠OAC,
∵$\frac{QA}{OA}$=$\frac{AB}{AC}$=$\frac{4}{3}$,
∴△QAB∽OAC,
∴BQ=$\frac{4}{3}$OC,
当BQ最小时,OC最小,
易知OA=3,AQ=4,OQ=5,BQ≥OQ-OB,
∴BQ≥2,
∴BQ的最小值为2,
∴OC的最小值为$\frac{3}{4}$×2=$\frac{3}{2}$,
故答案为$\frac{3}{2}$.
点评 本题考查圆综合题、全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理.三角形的三边关系等知识,解题的关键是学会利用旋转法添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案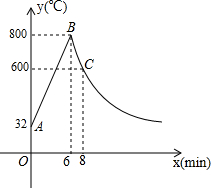 如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.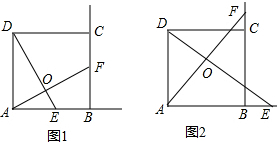
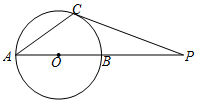 如图,点C在⊙O上,过点C作⊙O的切线,与直径AB的延长线交于点P,连接AC,若∠A=35°,则∠P=20度.
如图,点C在⊙O上,过点C作⊙O的切线,与直径AB的延长线交于点P,连接AC,若∠A=35°,则∠P=20度. 如图,点A、B、E、D在同一直线上,AC∥DF,AE=BD,AC=DF.
如图,点A、B、E、D在同一直线上,AC∥DF,AE=BD,AC=DF.