题目内容
10.若(m-2)2+$\sqrt{n+3}$=0,则m-n=5.分析 直接利用算术平方根的性质以及结合偶次方的性质得出m,n的值,即可得出答案.
解答 解:∵(m-2)2+$\sqrt{n+3}$=0,
∴m-2=0,n+3=0,
解得:m=2,n=-3,
故m-n=2-(-3)=5.
故答案为:5.
点评 此题主要考查了算术平方根的性质和偶次方的性质,正确掌握算术平方根的性质是解题关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
19.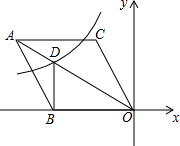 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
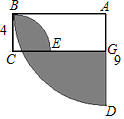 以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为$\frac{97}{4}$π-36.
以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为$\frac{97}{4}$π-36.
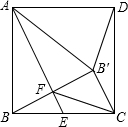 在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )
在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )