题目内容
14. 如图,点A、B、E、D在同一直线上,AC∥DF,AE=BD,AC=DF.
如图,点A、B、E、D在同一直线上,AC∥DF,AE=BD,AC=DF.求证:∠C=∠F.
分析 先根据平行线的性质,以及等式性质,得出∠A=∠D,AB=DE,进而判定△ABC≌△DEF,进而得出∠C=∠F.
解答  证明:∵AC∥DF,
证明:∵AC∥DF,
∴∠A=∠D,
∵AE=BD,
∴AE=BE=BD-BE,
即AB=DE,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AC=DF}\\{∠A=∠D}\\{AB=DE}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴∠C=∠F.
点评 本题考查全等三角形的判定和性质、平行线的性质,解题的关键是熟练掌握全等三角形的判定方法.

练习册系列答案
相关题目
19.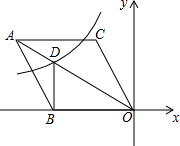 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
3.为推进黄石经济社会转型,2016年9月26日我市举办了主题为“转型黄石•灵秀湖 北”的园博会.据 悉,举办该会总共投资了7.65亿元.其中7.65亿元用科学记数法表示是( )
| A. | 7.65×108 | B. | 76.5×107 | C. | 0.765×109 | D. | 765×106 |
10. 如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
 如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )| A. | 变大 | B. | 先变大后变小 | C. | 先变小后变大 | D. | 不变 |

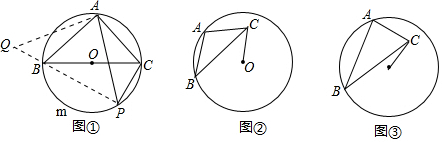
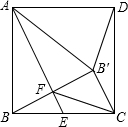 在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )
在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )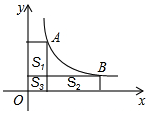 如图,A、B是双曲线y=$\frac{k}{x}$上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k=3.
如图,A、B是双曲线y=$\frac{k}{x}$上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k=3.