题目内容
 在平面直角坐标系中,0为坐标原点,A(-2,3).B (2,2)
在平面直角坐标系中,0为坐标原点,A(-2,3).B (2,2)(1)画出三角形OAB;
(2)求三角形OAB的面积即 S三角形OAB的值;
(3)若三角形OAB中任意一点P(x0,y0)经平移后对应点为P1(x0+4,y0-3).请画出三角形OAB平移后得到的三角形O1A1B1,并写出点01、A1、B1的坐标.
考点:作图-平移变换
专题:
分析:(1)根据平面直角坐标系找出点A、B的位置,然后与点O顺次连接即可;
(2)根据三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解;
(3)根据点P、P1的坐标确定出平移规律,然后找出点O、A、B的对应点01、A1、B1的位置,再顺次连接即可,最后根据平面直角坐标系写出各点的坐标.
(2)根据三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解;
(3)根据点P、P1的坐标确定出平移规律,然后找出点O、A、B的对应点01、A1、B1的位置,再顺次连接即可,最后根据平面直角坐标系写出各点的坐标.
解答: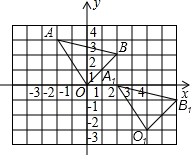 解:(1)△OAB如图所示;
解:(1)△OAB如图所示;
(2)S△OAB=3×4-
×2×3-
×2×2-
×1×4
=12-3-2-2
=12-7
=5;
(3)∵P(x0,y0)经平移后对应点为P1(x0+4,y0-3),
∴平移规律为向右4个单位,向下3个单位,
△O1A1B1如图所示,
01(4,-3),A1(2,0),B1(6,-1).
 解:(1)△OAB如图所示;
解:(1)△OAB如图所示;(2)S△OAB=3×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=12-3-2-2
=12-7
=5;
(3)∵P(x0,y0)经平移后对应点为P1(x0+4,y0-3),
∴平移规律为向右4个单位,向下3个单位,
△O1A1B1如图所示,
01(4,-3),A1(2,0),B1(6,-1).
点评:本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
在下列图形中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
某冶炼厂进口的某种稀有矿石这个月的进口量比上个月减少了5%,由于国际这种矿石价格上涨,这个月进口矿石的费用反而比上个月增加14%,则这个月的矿石价格相对上个月的增长率是( )
| A、25% | B、20% |
| C、15% | D、10% |
由x>y可以得到ax≤ay,下列条件正确的是( )
| A、a>0 | B、a<0 |
| C、a≤0 | D、a≥0 |

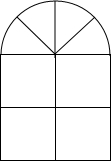 如图,一个窗户的上部是由四个扇形组成的一个半径为R的半圆,下部是边长相同的四个小正方形.
如图,一个窗户的上部是由四个扇形组成的一个半径为R的半圆,下部是边长相同的四个小正方形.