题目内容
14.如图1,边长为m的正方形OBCD的顶点O在坐标原点处,点B、D分别在y轴、x轴上,点A是DO边上的动点(不与点O、D重合),∠CAG=90°,且AG与正方形的外角平分线OI交于点E,线段OA的长为n(1)若|$\sqrt{m-1}$-2|+$\sqrt{2-n}$=0,求m和n的值;
(2)在(1)的条件下求出E点坐标;
(3)如图2,连接CE交y轴于点F,当BF=OF时,求OA:AD的值.

分析 (1)根据题意得:$\sqrt{m-1}$-2=0,2-n=0,即可求出m、n的值;
(2)作EM⊥x轴于M,设OM=EM=x,证明△ADC∽△EMA,得出比例式求出x,即可得出结果;
(3)作EM⊥x轴于M,在CD上截取DH=DA,连接AH,延长CE交x轴于N,先证明△AHC≌△EOA,得出AC=EA,再证明△ADC≌△EMA,得出AD=EM,再由BC∥ON,BF=OF,得出比例式$\frac{ON}{BC}=\frac{NF}{CF}=\frac{OF}{BF}$=1,得出ON=BC,OF=$\frac{1}{2}$ON,设EM=OM=x,则MN=2x,AD=EM=x,求出OA=2x,AD=x,即可得出结果.
解答 解:(1)∵|$\sqrt{m-1}$-2|+$\sqrt{2-n}$=0,
∴$\sqrt{m-1}$-2=0,2-n=0,
∴m=5,n=2;
(2)作EM⊥x轴于M,如图1所示: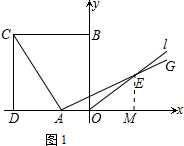 ∵m=5,n=2,
∵m=5,n=2,
∴OD=CD=5,OA=2,
∵OE平分∠BOM,
∴∠EOM=45°,
∴EM=OM,
设OM=EM=x,
∵∠CAG=90°,
∴∠DAC+∠DCA=90°,
∵∠DAC+∠MAE=90°,
∴∠DCA=∠MAE,
∴△ADC∽△EMA,
∴$\frac{AD}{EM}=\frac{CD}{AM}$,即$\frac{3}{x}=\frac{5}{2+x}$,
解得:x=3,
∴OM=EM=3,
∴E点坐标为(3,3);
(3)作EM⊥x轴于M,在CD上截取DH=DA,连接AH,延长CE交x轴于N,如图2所示: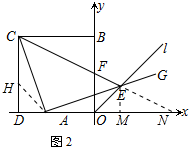 则CH=AO,
则CH=AO,
∵∠ODC=90°,
∴∠DHA=45°,
∴∠CHA=135°,
∵∠AOE=180°-45°=135°,
∴∠CHA=∠AOE,
在△AHC和△EOA中,$\left\{\begin{array}{l}{∠DCA=∠MAE}&{\;}\\{CH=AO}&{\;}\\{∠CHA=∠AOE}&{\;}\end{array}\right.$,
∴△AHC≌△EOA(ASA),
∴AC=EA,
在△ADC和△EMA中,$\left\{\begin{array}{l}{∠DCA=∠MAE}&{\;}\\{∠ADC=∠EMA=90°}&{\;}\\{AC=EA}&{\;}\end{array}\right.$,
∴△ADC≌△EMA(AAS),
∴AD=EM,
∵BC∥ON,BF=OF,
∴$\frac{ON}{BC}=\frac{NF}{CF}=\frac{OF}{BF}$=1,
∴ON=BC,
∴OF=$\frac{1}{2}$ON,
∵$\frac{EM}{MN}=\frac{OF}{ON}$=$\frac{1}{2}$,
∴$\frac{OM}{MN}=\frac{1}{2}$,
设EM=OM=x,则MN=2x,AD=EM=x,
∴OD=BC=ON=3x,
∴OA=2x,
∴OA:AD=2:1.
点评 本题是四边形综合题,主要考查了正方形的性质、相似三角形的判定与性质、全等三角形的判定与性质等知识;本题难度较大,综合性强,特别是(3)中,通过作辅助线证明两次三角形全等以及由平行线得出比例式才能得出结论.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. |  | B. |  | C. |  | D. |  |
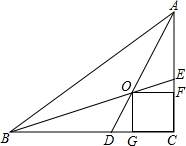 如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.
如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.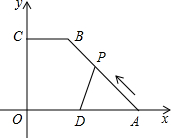 已知,如图,在直角梯形COAB中,CB∥OA,以O为原点建立平面直角坐标系,A、B、C的坐标分别为A(10,0)、B(4,8)、C(0,8),D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒,
已知,如图,在直角梯形COAB中,CB∥OA,以O为原点建立平面直角坐标系,A、B、C的坐标分别为A(10,0)、B(4,8)、C(0,8),D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒,