题目内容
16.如图①,已知线段AB=12cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点.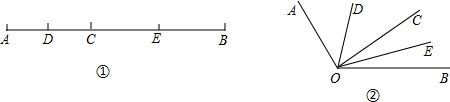
(1)若点C恰为AB的中点,则DE=6cm;
(2)若AC=4cm,则CE,DE的长;
(3)当点C为线段AB上任一点,其它条件不变,试利用“字母代替数”的方法,说明DE与AB至今的关系,写出你的结论并证明理由.
(4)知识迁移:如图②,过∠AOB的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,
若∠AOB=100°,则∠DOE=50度(直接写出结果).
若∠AOB=n°,则∠DOE=$\frac{1}{2}$n度(直接写出结果).
分析 (1)根据线段中点的性质计算即可;
(2)根据线段中点的性质和给出的数据,结合图形计算;
(3)同(1)的解法相同;
(4)根据角平分线的定义进行解答即可.
解答 解:(1)∵点D,E分别是AC和BC的中点,
∴DC=$\frac{1}{2}$AC,CE=$\frac{1}{2}$CB,
∴DC+CE=$\frac{1}{2}$(AC+CB)=6cm;
故答案为:6.
(2)∵AC=4cm,
∴CD=2cm,
∵AB=12cm,AC=4cm,
∴BC=8cm,
∴CE=4cm,DE=DC+CE=6cm;
(3))∵点D,E分别是AC和BC的中点,
∴DC=$\frac{1}{2}$AC,CE=$\frac{1}{2}$CB,
∴DC+CE=$\frac{1}{2}$(AC+CB),
即DE=$\frac{1}{2}$AB;
(4)∵OD,OE分别平分∠AOC和∠BOC,
∴∠DOC=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠COB,
∴∠DOE=∠DOC+∠COE=$\frac{1}{2}$∠AOB=50°,
当∠AOB=n°,∠DOE=$\frac{1}{2}$n°.
故答案为:50;$\frac{1}{2}$n.
点评 本题考查的是线段的计算和角的计算,掌握线段中点的性质和角平分线的定义是解题的关键,注意类比思想的应用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
1.下列句子,不一定正确的是( )
| A. | 若a=b,则a+c=b+c | B. | 若a+c=b+c,则a=b | C. | 若a=b,则ac=bc | D. | 若ac=bc,则a=b |
6.下列运算正确的是( )
| A. | x3•x2=x6 | B. | 2a+3b=5ab | C. | a3÷a2=a(a≠0) | D. | (ab2)3=ab6 |
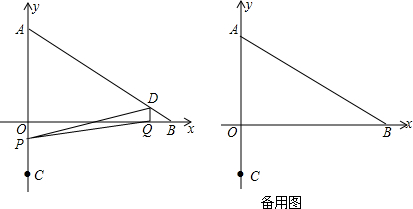
 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限内,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=ax2+ax-5经过点B.
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限内,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=ax2+ax-5经过点B.
 如图,∠B=∠D=90°,请补充一个条件:AB=AD,使△ABC≌△ADC.
如图,∠B=∠D=90°,请补充一个条件:AB=AD,使△ABC≌△ADC. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.