题目内容
12．在Rt△ABC中，CD是斜边AB上的高，若∠B=30°，AD=2，则AB=8．分析 先由含30°角的直角三角形的性质得出AB=2AC，再求出∠A，得出∠ACD=30°，由含30°角的直角三角形的性质得出AC=2AD=4，即可得出AB的长．
解答 解：如图所示：
∵∠ACB=90°，∠B=30°，
∴AB=2AC，∠A=90°-30°=60°，
∵CD是斜边AB上的高，
∴∠CDA=90°，
∴∠ACD=90°-∠A=30°，
∴AC=2AD=4，
∴AB=2AC=8，
故答案为：8．
点评 本题考查了含30°角的直角三角形的性质、直角三角形的两个锐角互余的性质；灵活运用含30°角的直角三角形的性质是解决问题的关键，本题难度适中．
练习册系列答案
相关题目
如图，A点坐标为（3，3），将△ABC先向下平移4个单位得△A1B1C1，再将△A1B1C1向左平移5个单位得△A2B2C2．
如图，写出△ABC的各顶点坐标，并画出△ABC关于y轴的对称图形△A1B1C1，再画出△A1B1C1向右平移1个单位的△A2B2C2．
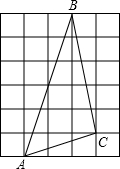如图，图中的小方格都是边长为1的正方形，若A（-x，$\frac{-3y+6}{2}$），B（2x-1，$\frac{2y+1}{3}$），C（z+1，$\frac{2z-8}{3}$），已知A、B关于原点对称，C在二、四象限平分线上．
已知：如图，在平面直角坐标系中，正方形ABCD的边长为8．求出AC和BD的长度，并直接写出它的四个顶点A、B、C、D的坐标．