题目内容
9. 阅读下面的材料:
阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)已知一次函数y=-2x的图象为直线l1,求过点P(1,4)且与已知直线l1平行的直线l2的函数表达式,并在坐标系中画出直线l1和l2的图象;
(2)设直线l2分别与y轴、x轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求l1和l2两平行线之间的距离OC的长;
(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标.
(4)在x轴上找一点M,使△BMP为等腰三角形,求M的坐标.(直接写出答案)
分析 (1)设直线l2的解析式为y=-2x+b,把点P(1,4)代入即可求得b的值,进而求得函数的解析式;
(2)首先求出A和B的坐标,然后根据三角形的面积公式求得;
(3)B关于y轴的对称点B'(-3,0),连结B'P交y轴于Q,求得PB'的解析式,则Q的坐标即可求得;
(4)分B、M和P分别是等腰三角形的顶角的顶点三种情况进行讨论,依据等腰三角形的性质即可求解.
解答 解:(1)∵l1∥l2,
∴设直线l2的解析式为y=-2x+b,
把点P(1,4)代入得,4=-2+b,b=6
∴y=-2x+6(1分),
画图如右图所示 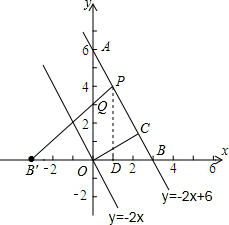
(2)直线l2与y轴、x轴的交点A、B的坐标,分别为(0,6),(3,0);
∵OA=6,OB=3,则AB=$3\sqrt{5}$,
又S△AOB=2OA×OB=AB×OC,
∴$OC=\frac{6}{{\sqrt{5}}}$(或$\frac{6}{5}\sqrt{5}$)
(3)∵B关于y轴的对称点B'(-3,0),连结B'P交y轴于Q,
∴QP+QB的最小值为$4\sqrt{2}$,
∵直线B'P的解析式为y=x+3,
∴Q(0,3),
(4)过P作PD⊥x轴于点D,则D的坐标是(1,0),当P是等腰△PBM的顶角顶点时,M的坐标是(-1,0);
在直角△PBD中,PB=$\sqrt{P{D}^{2}+B{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
则当B是等腰△PBM的顶角的顶点时,M的坐标是(3+2$\sqrt{5}$,0)或M(3-2$\sqrt{5}$,0);
PB的中点是(2,2),设过(2,2)且与AB垂直的直线的解析式是:y=$\frac{1}{2}$x+c,
则1+c=2,
解得:c=1,
则函数的解析式是y=$\frac{1}{2}$x+1.
当y=0时,$\frac{1}{2}$x+1=0,解得:x=-2.
则M的坐标是(-2,0).
总之,M(-1,0)或M(-2,0)或M(3+2$\sqrt{5}$,0)或M(3-2$\sqrt{5}$,0).
点评 本题考查了待定系数法求函数的解析式,以及等腰三角形的性质,正确进行讨论是本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
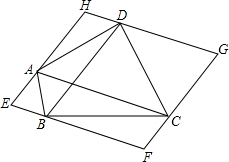 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,得到四边形EFGH.
如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,得到四边形EFGH.
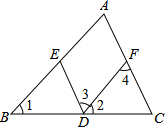 如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.
如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.