题目内容
17.已知等腰三角形ABC的底边BC=12cm,其面积S△ABC=12$\sqrt{3}$cm2,求△ABC的三个内角的度数.分析 过A作AD⊥BC于D,利用等腰三角形三线合一的性质得到BD=CD,根据已知面积,由BC的长求出AD的长,在直角三角形ABD中,利用锐角三角函数定义求出tanB的值,确定出∠B的度数,再根据等腰三角形两底角相等得出∠C=∠B,利用三角形内角和定理求出∠BAC.
解答 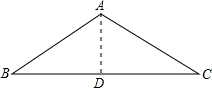 解:如图,过A作AD⊥BC于D,
解:如图,过A作AD⊥BC于D,
∵AB=AC,
∴BD=CD=$\frac{1}{2}$BC=6cm,
∵S△ABC=12$\sqrt{3}$cm2,
∴$\frac{1}{2}$BC•AD=6AD=12$\sqrt{3}$,
∴AD=2$\sqrt{3}$cm,
在Rt△ABD中,∵tanB=$\frac{AD}{BD}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠B=30°,
∴∠C=∠B=30°,∠BAC=120°,
即△ABC的三个内角的度数分别是∠BAC=120°,∠B=∠C=30°.
点评 此题考查了解直角三角形,涉及的知识点有:等腰三角形的性质,三角形的面积,锐角三角函数定义,特殊角的三角函数值,三角形内角和定理,求出∠B的度数是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.下列命题是假命题的是( )
| A. | 对顶角相等 | B. | -4是有理数 | ||
| C. | 内错角相等 | D. | 两个等腰直角三角形相似 |
 如图所示,BD平分∠ABC,BE将∠ABD分成角度为2:5的两部分,∠DBE=20°,求∠ABC的度数.
如图所示,BD平分∠ABC,BE将∠ABD分成角度为2:5的两部分,∠DBE=20°,求∠ABC的度数. 如图,观察时钟,在2时和3时之间什么时刻,时针和分针的夹角为直角?
如图,观察时钟,在2时和3时之间什么时刻,时针和分针的夹角为直角?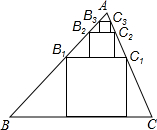 如图,在△ABC中,BC=6,S△ABC=12,B1C1所在四边形是△ABC的内接正方形,B2C2所在四边形是△AB1C1的内接正方形,B3C3所在四边形是△AB2C2的内接正方形,依此类推,则BnCn的长为6×($\frac{2}{5}$)n.
如图,在△ABC中,BC=6,S△ABC=12,B1C1所在四边形是△ABC的内接正方形,B2C2所在四边形是△AB1C1的内接正方形,B3C3所在四边形是△AB2C2的内接正方形,依此类推,则BnCn的长为6×($\frac{2}{5}$)n. 如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F.
如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F.