Question

3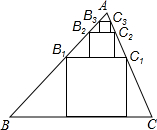．如图，在△ABC中，BC=6，S_△ABC=12，B₁C₁所在四边形是△ABC的内接正方形，B₂C₂所在四边形是△AB₁C₁的内接正方形，B₃C₃所在四边形是△AB₂C₂的内接正方形，依此类推，则B_nC_n的长为6×（$\frac{2}{5}$）ⁿ．

Answer 1

分析 过点A作AD⊥BC于点D，交B₁C₁于点E，交B₂C₂于点F，由B₁C₁所在四边形是△ABC的内接正方形，易证得△AB₁C₁∽△ABC，由在△ABC中，BC=6，S_△ABC=12，可求得高AD的长，然后由相似三角形对应高的比等于相似比，求得B₁C₁的长，同理可求得B₂C₂与B₃C₃的长，观察即可得规律：B_nC_n=6×（$\frac{2}{5}$）ⁿ．

解答 解：过点A作AD⊥BC于点D，交B₁C₁于点E，交B₂C₂于点F，
∵B₁C₁所在四边形是△ABC的内接正方形，
∴B₁C₁∥BC，AD⊥B₁C₁，ED=B₁C₁，
∴△AB₁C₁∽△ABC，
∵在△ABC中，BC=6，S_△ABC=12，
∴AD=4，
设B₁C₁=x，则AE=4-x，
∴$\frac{AE}{AD}=\frac{{B}_{1}{C}_{1}}{BC}$，
即：$\frac{4-x}{4}=\frac{x}{6}$，
解得：x=$\frac{12}{5}$，
即B₁C₁=$\frac{12}{5}$；
同理：△AB₂C₂∽△AB₁C₁，
∴$\frac{AF}{AE}=\frac{{B}_{2}{C}_{2}}{{B}_{1}{C}_{1}}$，
∵AE=4-$\frac{12}{5}$=$\frac{8}{5}$，
∴设B₂C₂=y，则AF=$\frac{8}{5}$-y，
∴$\frac{\frac{8}{5}-y}{\frac{8}{5}}=\frac{y}{\frac{12}{5}}$，
解得：y=$\frac{24}{25}$，
即B₂C₂=$\frac{24}{25}$=6×（$\frac{2}{5}$）²；
同理：B₃C₃=6×（$\frac{2}{5}$）³；
∴B_nC_n=6×（$\frac{2}{5}$）ⁿ．
故答案为：6×（$\frac{2}{5}$）ⁿ．

点评 此题考查了相似三角形的判定与性质，正方形的性质，平行线的性质，熟练掌握相似三角形的判定和性质是解题的关键．