题目内容
1.矩形ABCD的对角线AC=8cm,∠AOD=120°,则CB的长为4$\sqrt{3}$cm.分析 由矩形的性质得出OA=OB=4cm,再证明△AOB是等边三角形,即可得出AB=OA=4cm,根据勾股定理求出CB即可.
解答 解:如图:∵四边形ABCD是矩形,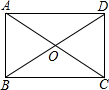
∴OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,BD=AC=8cm,∠ABC=90°,
∴OA=OB=4cm,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=4cm,
在Rt△ABC中,由勾股定理得:BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$(cm),
故答案为:4$\sqrt{3}$.
点评 本题考查了矩形的性质、勾股定理、等边三角形的判定与性质;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
20.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | 2 |
16.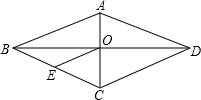 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
6.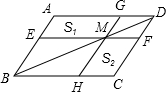 如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )
如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )
 如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )
如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 不能确定 |
13.已知(m+n)2=5,mn=1,则m2+n2的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
10.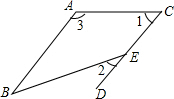 下图中能用一个字母表示的角( )
下图中能用一个字母表示的角( )
 下图中能用一个字母表示的角( )
下图中能用一个字母表示的角( )| A. | 三个 | B. | 四个 | C. | 五个 | D. | 没有 |
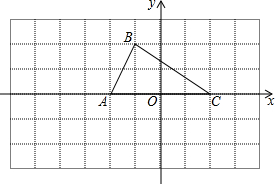 如图,已知△ABC的三个顶点的坐标分别为A(-2,0),B(-1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标(3,2),(-5,2),(1,-2).
如图,已知△ABC的三个顶点的坐标分别为A(-2,0),B(-1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标(3,2),(-5,2),(1,-2).
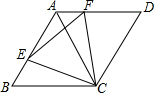 如图,菱形ABCD,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求∠ECF的度数.
如图,菱形ABCD,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求∠ECF的度数.