题目内容
8.某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
分析 (1)用喜欢跳绳的人数除以其所占的百分比即可求得被调查的总人数;
(2)用总人数乘以足球所占的百分比即可求得喜欢足球的人数,用总数减去其他各小组的人数即可求得喜欢跑步的人数,从而补全条形统计图;
(3)用样本估计总体即可确定最喜爱篮球的人数比最喜爱足球的人数多多少.
解答 解:(1)观察条形统计图与扇形统计图知:喜欢跳绳的有10人,占25%,
故总人数有10÷25%=40人;
(2)喜欢足球的有40×30%=12人,
喜欢跑步的有40-10-15-12=3人,
故条形统计图补充为: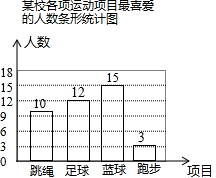
(3)全校最喜爱篮球的人数比最喜爱足球的人数多1200×$\frac{15-12}{40}$=90人.
点评 本题考查了扇形统计图、条形统计图及用样本估计总体的知识,解题的关键是能够读懂两种统计图并从中整理出进一步解题的有关信息,难度不大.

练习册系列答案
相关题目
16.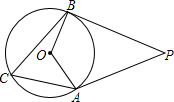 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )
 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )| A. | 65° | B. | 130° | C. | 50° | D. | 100° |
20.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | 2 |
10.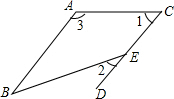 下图中能用一个字母表示的角( )
下图中能用一个字母表示的角( )
 下图中能用一个字母表示的角( )
下图中能用一个字母表示的角( )| A. | 三个 | B. | 四个 | C. | 五个 | D. | 没有 |
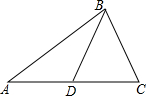 如图,BD是△ABC的中线,AB⊥BC,AD=2,AB=6,BC=3,则△ABD的面积是4.5.
如图,BD是△ABC的中线,AB⊥BC,AD=2,AB=6,BC=3,则△ABD的面积是4.5.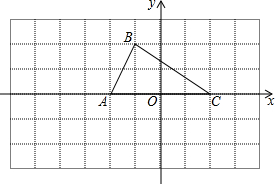 如图,已知△ABC的三个顶点的坐标分别为A(-2,0),B(-1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标(3,2),(-5,2),(1,-2).
如图,已知△ABC的三个顶点的坐标分别为A(-2,0),B(-1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标(3,2),(-5,2),(1,-2). 如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.
如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.