题目内容
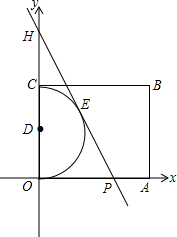 如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E.
如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E.(1)求切线PH所在直线的解析式;
(2)求线段OP、EP与弧OE所围成图形的面积S.
考点:圆的综合题
专题:
分析:(1)设切线PH所在直线的解析式为y=kx+b,连接DE,DP,利用已知条件和勾股定理可求出OP,OH的长,即点P和点H的坐标,代入直线解析式求出k和b的值即可;
(2)易证Rt△OPD≌Rt△EPD,由全等三角形的性质可求出∠ODE的度数,再根据线段OP、EP与弧OE所围成图形的面积S=2S△OPD-S扇形DOE计算即可.
(2)易证Rt△OPD≌Rt△EPD,由全等三角形的性质可求出∠ODE的度数,再根据线段OP、EP与弧OE所围成图形的面积S=2S△OPD-S扇形DOE计算即可.
解答:解:(1)连接DE,DP,
∵四边形OABC是矩形,
∴∠DOP=90°
∵OC是圆的半径,
∴OP切圆D于点O,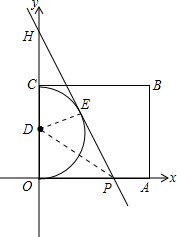
∴PH与半圆D切于点E,
∴OP=EP,∠DPO=∠DPE=
∠OPH=30°,∠OHP=90°-∠OPH=30°,
∴DP=2OD=4,
OP=
=2
,HP=2OP=4
,
∴OH=
=6,
∴P(2
,0),H(0,6),
设切线PH所在直线的解析式为y=kx+b(k≠0),
把P,H点的坐标代入得:
,
解得:
,
∴切线PH所在直线的解析式为y=-
x++6;
(2)在Rt△OPD和Rt△EPD中,
,
∴Rt△OPD≌Rt△EPD,
∴∠ODP=∠EDP=90°-∠OPD=60°,
∴∠ODE=120°,
∴线段OP、EP与弧OE所围成图形的面积S=2S△OPD-S扇形DOE=2×
×2
×2-
=4
-
.
∵四边形OABC是矩形,
∴∠DOP=90°
∵OC是圆的半径,
∴OP切圆D于点O,

∴PH与半圆D切于点E,
∴OP=EP,∠DPO=∠DPE=
| 1 |
| 2 |
∴DP=2OD=4,
OP=
| DP2-OD2 |
| 3 |
| 3 |
∴OH=
| PH2-OP2 |
∴P(2
| 3 |
设切线PH所在直线的解析式为y=kx+b(k≠0),
把P,H点的坐标代入得:
|
解得:
|
∴切线PH所在直线的解析式为y=-
| 3 |
(2)在Rt△OPD和Rt△EPD中,
|
∴Rt△OPD≌Rt△EPD,
∴∠ODP=∠EDP=90°-∠OPD=60°,
∴∠ODE=120°,
∴线段OP、EP与弧OE所围成图形的面积S=2S△OPD-S扇形DOE=2×
| 1 |
| 2 |
| 3 |
| 120×π×22 |
| 360 |
| 3 |
| 4π |
| 3 |
点评:本题考查了和圆有关的综合题,用到的知识点有矩形的性质、切线长定理、勾股定理、用待定系数法求一次函数解析式、全等三角形的判定和性质以及三角形的面积公式、扇形的面积公式运用,题目的综合性较强,难度中等.

练习册系列答案
相关题目
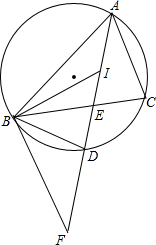 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D、BC于点E.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D、BC于点E. 如图,⊙O是△ABC的外接圆,且AB=AC=5,BC=8,则⊙O的半径为
如图,⊙O是△ABC的外接圆,且AB=AC=5,BC=8,则⊙O的半径为 如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.
如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.