题目内容
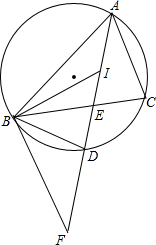 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D、BC于点E.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D、BC于点E.(1)求证:BD=ID;
(2)若ID=4,AD=8,求DE的长;
(3)延长ID至点F,使DF=ID.连结BF,求证:BF⊥BI.
考点:圆的综合题
专题:证明题
分析:(1)要证明ID=BD,只要求得∠BID=∠IBD即可;
(2)根据已知及相似三角形的判定方法得到△ABD∽△BED,由相似三角形的性质:对应边的比值相等即可求出DE的长;
(3)由(1)可知ID=BD,所以BD=ID=DF,即BD=
ID,所以三角形BFI是直角三角形,进而可证明BF⊥BI.
(2)根据已知及相似三角形的判定方法得到△ABD∽△BED,由相似三角形的性质:对应边的比值相等即可求出DE的长;
(3)由(1)可知ID=BD,所以BD=ID=DF,即BD=
| 1 |
| 2 |
解答:(1)证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD;
(2)解:∵∠BAD=∠CBD=∠EBD,∠D=∠D,
∴△ABD∽△BED,
∴BD:DE=AD:BD,
∵ID=BD=4,AD=8,
∴4:DE=8:4,
∴DE=2;
(3)∵ID=BD,DF=ID,
∴BD=ID=DF,
即BD=
ID,
∴△BFI是直角三角形,
∴BF⊥BI.
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD;
(2)解:∵∠BAD=∠CBD=∠EBD,∠D=∠D,
∴△ABD∽△BED,
∴BD:DE=AD:BD,
∵ID=BD=4,AD=8,
∴4:DE=8:4,
∴DE=2;
(3)∵ID=BD,DF=ID,
∴BD=ID=DF,
即BD=
| 1 |
| 2 |
∴△BFI是直角三角形,
∴BF⊥BI.
点评:本题考查了三角形的内心的性质,以及等腰三角形的判定与性质,相似三角形的判定与性质,直角三角形的判定和性质,证明△ABD∽△BED是解题关键.

练习册系列答案
相关题目
 如图,△ABC的三个顶点均在正方形网格的格点上,则tanB的值为( )
如图,△ABC的三个顶点均在正方形网格的格点上,则tanB的值为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
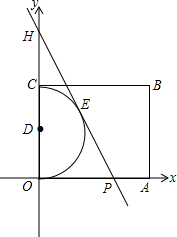 如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E.
如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E. 如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积.
如图,四边形ABCD中,过点D作DE⊥AB,作DF⊥BC,垂足分别为点E、F,∠EDF=60°,若BE=14,BF=2,求平行四边形ABCD的周长和面积. 求证:同弧或等弧所对的圆周角都相等.(求证:∠ADB=∠ACB)
求证:同弧或等弧所对的圆周角都相等.(求证:∠ADB=∠ACB)