Question

已知：如图矩形ABCD中，AB=2，BC=1，先折出折痕（对角线）BD，再折叠使AD边与对角线BD重合，得折痕DG，求AG的长．

Answer 1

考点：翻折变换（折叠问题）,勾股定理,矩形的性质

专题：

分析：已知AB=2，BC=1，可知AD=BC=1，在Rt△ABD中用勾股定理求BD；设AG=x，由折叠的性质可知，则GE=x，BG=2-x，在Rt△EBG中，用勾股定理列方程求x即可．

解答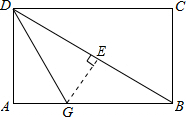：解：作GE⊥DB于点E，
由折叠的性质可知：△ADG≌△EDG，
∴DE=1，AG=GE，
∵∠A=90°，
∴DB=

AD2+AB2

=

5

，
∴EB=

5

-1，
设AG=x，则GE=x，BG=2-x，在Rt△EBG中，
x²+（

5

-1）²=（2-x）²，
解得：x=

5 -1

2

，
即AG的长为

5 -1

2

．

点评：本题考查了图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应线段相等．同时考查了勾股定理在折叠问题中的运用．