题目内容
6.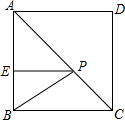 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3,P是AC上一动点,则PB+PE的最小值是$\sqrt{34}$.
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3,P是AC上一动点,则PB+PE的最小值是$\sqrt{34}$.
分析 由正方形的性质得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
解答 解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3,
∴AE=3,AB=5,
∴DE=$\sqrt{{3}^{2}+{5}^{2}}=\sqrt{34}$,
故PB+PE的最小值是$\sqrt{34}$.
故答案为:$\sqrt{34}$
点评 本题考查了轴对称-最短路线问题,正方形的性质,解此题通常是利用两点之间,线段最短的性质得出.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.下列说法不正确的是( )
| A. | 0.4的算术平方根是0.2 | B. | -9是81的一个平方根 | ||
| C. | -27的立方根是-3 | D. | 1-$\sqrt{2}$的相反数是$\sqrt{2}$-1 |
14.在x=1,y=5x,x2=0,xy=2这四个方程中,是一元一次方程的是( )
| A. | x=1 | B. | y=5x | C. | x2=0 | D. | xy=2 |
11.某种病毒的直径是0.000018毫米,0.000018这个数用科学记数法表示为( )
| A. | 18×10-6 | B. | 1.8×10-6 | C. | 0.18×10-4 | D. | 1.8×10-5 |
 如图,正方形ABCD的面积为$\sqrt{10}$,则图中阴影部分的面积为$\frac{\sqrt{10}}{2}$.
如图,正方形ABCD的面积为$\sqrt{10}$,则图中阴影部分的面积为$\frac{\sqrt{10}}{2}$.