题目内容
 如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.
如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.(1)求证:CE=CF;
(2)若点G在AD边上,且∠GCE=45°,BE=3,DG=5,求GE的长.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得BC=DC,∠B=∠FDC=90°,再证明△CBE≌△CDF可得CE=CF;
(2)首先证明∠GCF=∠GCE,然后证明△ECG≌△FCG,根据全等三角形的性质可得GE=GF=DG+DF=DG+BE=3+5=8.
(2)首先证明∠GCF=∠GCE,然后证明△ECG≌△FCG,根据全等三角形的性质可得GE=GF=DG+DF=DG+BE=3+5=8.
解答:(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠B=∠FDC=90°,
在△EBC和△FDC中,
,
∴△CBE≌△CDF(SAS),
∴CE=CF;
(2)解:由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵在△ECG≌△FCG中,
,
∴△ECG≌△FCG(SAS),
∴GE=GF=DG+DF=DG+BE=3+5=8.
∴BC=DC,∠B=∠FDC=90°,
在△EBC和△FDC中,
|
∴△CBE≌△CDF(SAS),
∴CE=CF;
(2)解:由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵在△ECG≌△FCG中,
|
∴△ECG≌△FCG(SAS),
∴GE=GF=DG+DF=DG+BE=3+5=8.
点评:此题主要考查了正方形的性质,关键是掌握正方形四边相等,四个角都是直角.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
 一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由
一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由
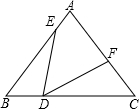 如图,△ABC,AB=AC=10,BC=12,点D在边BC,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交射线CA于点F
如图,△ABC,AB=AC=10,BC=12,点D在边BC,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交射线CA于点F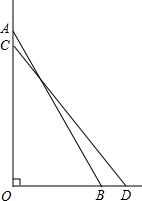 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.

