题目内容
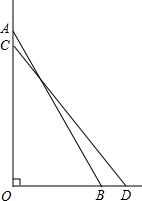 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
考点:解直角三角形的应用
专题:几何图形问题
分析:设梯子的长为xm.在Rt△ABO中,根据三角函数得到OB,在Rt△CDO中,根据三角函数得到OD,再根据BD=OD-OB,得到关于x的方程,解方程即可求解.
解答:解:设梯子的长为xm.
在Rt△ABO中,cos∠ABO=
,
∴OB=AB•cos∠ABO=x•cos60°=
x.
在Rt△CDO中,cos∠CDO=
,
∴OD=CD•cos∠CDO=x•cos51°18′≈0.625x.
∵BD=OD-OB,
∴0.625x-
x=1,
解得x=8.
故梯子的长是8米.
在Rt△ABO中,cos∠ABO=
| OB |
| AB |
∴OB=AB•cos∠ABO=x•cos60°=
| 1 |
| 2 |
在Rt△CDO中,cos∠CDO=
| OD |
| CD |
∴OD=CD•cos∠CDO=x•cos51°18′≈0.625x.
∵BD=OD-OB,
∴0.625x-
| 1 |
| 2 |
解得x=8.
故梯子的长是8米.
点评:此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
 如图,将一个正六边形分割成六个全等的等边三角形,其中有两个已涂灰,如果再随意涂灰一个空白三角形,则所有涂灰部分恰好成为一个轴对称图形的概率是( )
如图,将一个正六边形分割成六个全等的等边三角形,其中有两个已涂灰,如果再随意涂灰一个空白三角形,则所有涂灰部分恰好成为一个轴对称图形的概率是( ) 已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(-1,0),对称轴为直线x﹦-2,点C是抛物线与y轴的交点,点D是抛物线上另一点,已知以OC为一边的矩形OCDE的面积为8.
已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(-1,0),对称轴为直线x﹦-2,点C是抛物线与y轴的交点,点D是抛物线上另一点,已知以OC为一边的矩形OCDE的面积为8. 如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.
如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF. 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,设点C的坐标为(0,m)且m<6,△ABC的面积为S,试问:
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,设点C的坐标为(0,m)且m<6,△ABC的面积为S,试问: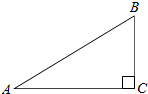 如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是
如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是