题目内容
20.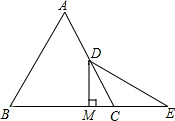 已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.
已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.(1)求∠E的度数.
(2)求证:BM=EM.
分析 (1)首先根据等边三角形的性质,可得∠ACB=60°,然后根据CE=CD,可得∠E=∠CDE;最后根据三角形的外角的性质,求出∠E的度数即可.
(2)首先连接BD,判断出∠ABC=2∠DBE,∠ACB=2∠E;然后根据∠ABC=∠ACB,判断出∠DBC=∠E,所以BD=DE,再根据DM⊥BE,判断出BM=EM即可.
解答 解:(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∵CE=CD,
∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,
∴∠ACB=2∠E,
∴∠E=60°÷2=30°.
即∠E的度数是30°.
(2)如图,连接BD,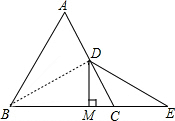 ,
,
∵△ABC是等边三角形,D是AC的中点,
∴BD是∠ABC的平分线,
∴∠ABC=2∠DBE;
∵CE=CD,
∴∠CED=∠CDE.
∵∠ACB=∠E+∠CDE,
∴∠ACB=2∠E;
∵∠ABC=∠ACB,
∴2∠DBC=2∠E,
∴∠DBC=∠E,
∴BD=DE,
∵DM⊥BE,
∴BM=EM.
点评 (1)此题主要考查了等边三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等边三角形的三个内角都相等,且都等于60°.
(2)此题还考查了等腰三角形的性质,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等;②等腰三角形的两个底角相等;③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(3)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:三角形的一个外角等于与它不相邻的两个内角和.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
10.二元一次方程组$\left\{\begin{array}{l}{x+2y=10}\\{y=2x}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ |
11. 如图,BD是⊙O的直径,弦AC⊥BD,垂足为E,∠AOB=60°,则∠BDC等于( )
如图,BD是⊙O的直径,弦AC⊥BD,垂足为E,∠AOB=60°,则∠BDC等于( )
 如图,BD是⊙O的直径,弦AC⊥BD,垂足为E,∠AOB=60°,则∠BDC等于( )
如图,BD是⊙O的直径,弦AC⊥BD,垂足为E,∠AOB=60°,则∠BDC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.某市在实数居民用水定额管理前,对居民生活用水情况进行了调查,如表是通过简单随机臭氧调查获得的50个家庭去年的月均用水量(单位:t)
(1)请选择合适的组距和组数.列出样本频数分布表,画出频数分布直方图,从直方图中你能得到什么信息?
(2)为了鼓励节约用水,要确定一个用水量的标准,抽出这个标准的部分按1.5倍价格收费,若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?
| 4.7 | 2.0 | 3.1 | 2.3 | 5.2 | 2.8 | 7.3 | 4.3 | 4.8 | 6.7 |
| 4.5 | 5.1 | 6.5 | 8.9 | 2.0 | 4.5 | 3.2 | 3.2 | 4.5 | 3.5 |
| 3.5 | 3.5 | 3.6 | 4.9 | 3.7 | 3.8 | 5.6 | 5.5 | 5.9 | 6.2 |
| 5.7 | 3.9 | 4.0 | 4.0 | 7.0 | 3.7 | 8.3 | 4.2 | 6.4 | 3.5 |
| 4.5 | 4.5 | 4.6 | 5.4 | 5.6 | 6.6 | 5.8 | 4.5 | 6.2 | 7.5 |
(2)为了鼓励节约用水,要确定一个用水量的标准,抽出这个标准的部分按1.5倍价格收费,若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?
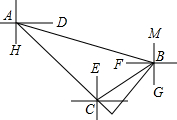 一艘巡逻艇从小岛B出发,沿北偏西75°方向航行10($\sqrt{3}$+1)海里到达A处时,收到由小岛B处求救中心发给它的指令,要求该巡逻艇30分钟内赶到海上C处进行救援,此时C处位于B处南偏西60°,位于巡逻艇南偏东45°,接到指令后巡逻艇立即以每小时50海里的速度赶往C处,问:巡逻艇能否在规定时间内赶到?
一艘巡逻艇从小岛B出发,沿北偏西75°方向航行10($\sqrt{3}$+1)海里到达A处时,收到由小岛B处求救中心发给它的指令,要求该巡逻艇30分钟内赶到海上C处进行救援,此时C处位于B处南偏西60°,位于巡逻艇南偏东45°,接到指令后巡逻艇立即以每小时50海里的速度赶往C处,问:巡逻艇能否在规定时间内赶到?