题目内容
17.(1)$\sqrt{9}$-$\sqrt{(-6)^{2}}$-$\root{3}{-27}$;(2)|$\sqrt{6}$-$\sqrt{3}$|-|3-$\sqrt{6}$|.
(3)x2-$\frac{121}{49}$=0.
分析 (1)首先求出每个算术平方根的大小,然后从左向右依次计算即可;
(2)首先根据绝对值的非负性化简,然后计算出算式|$\sqrt{6}$-$\sqrt{3}$|-|3-$\sqrt{6}$|的值是多少即可;
(3)首先根据x2-$\frac{121}{49}$=0,可得x2=$\frac{121}{49}$;然后根据一个正数有两个平方根,这两个平方根互为相反数,求出x的值是多少即可.
解答 解:(1)$\sqrt{9}$-$\sqrt{(-6)^{2}}$-$\root{3}{-27}$
=3-6-(-3)
=-3+3
=0
(2)|$\sqrt{6}$-$\sqrt{3}$|-|3-$\sqrt{6}$|
=$\sqrt{6}$-$\sqrt{3}$-(3-$\sqrt{6}$)
=$\sqrt{6}$-$\sqrt{3}$-3+$\sqrt{6}$
=2$\sqrt{6}$-$\sqrt{3}$-3
(3)∵x2-$\frac{121}{49}$=0,
∴x2=$\frac{121}{49}$,
解得x=±$\frac{11}{7}$.
故答案为:0;2$\sqrt{6}-\sqrt{3}$-3;±$\frac{11}{7}$.
点评 (1)此题主要考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
(2)此题还考查了绝对值的非负性质的应用,要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知$\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$是方程组$\left\{{\begin{array}{l}{ax+by+6=0}\\{bx-ay+7=0}\end{array}}\right.$的解,则a、b分别为( )
| A. | $\left\{{\begin{array}{l}{a=4}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{a=-4}\\{b=-1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{a=-4}\\{b=1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{a=4}\\{b=-1}\end{array}}\right.$ |
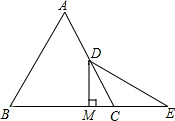 已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.
已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.