题目内容
12.已知$\frac{x+4}{x(x-2)}$=$\frac{A}{x-2}$-$\frac{B}{x}$,则常数A=3,B=1.分析 首先将原式通分,进而得出A-B=1,2B=4,求出即可.
解答 解:∵$\frac{x+4}{x(x-2)}$=$\frac{A}{x-2}$-$\frac{B}{x}$,
∴$\frac{x+4}{x(x-2)}$=$\frac{A}{x-2}$-$\frac{B}{x}$=$\frac{(A-B)x+2B}{(x-2)x}$,
∴A-B=1,2B=4,
∴A=3,B=1.
故答案为:3,1.
点评 此题主要考查了分式的加减运算,正确进行通分运算是解题关键.

练习册系列答案
相关题目
12.已知$\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$是方程组$\left\{{\begin{array}{l}{ax+by+6=0}\\{bx-ay+7=0}\end{array}}\right.$的解,则a、b分别为( )
| A. | $\left\{{\begin{array}{l}{a=4}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{a=-4}\\{b=-1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{a=-4}\\{b=1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{a=4}\\{b=-1}\end{array}}\right.$ |
10.若ax=6,ay=4,则a2x+y的值为( )
| A. | 104 | B. | 134 | C. | 144 | D. | 40 |
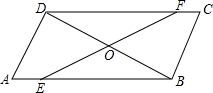 如图,?ABCD中,点E、F分别在AB、CD上,且AE=CF,EF与BD相交于点O,求证:OB=OD.
如图,?ABCD中,点E、F分别在AB、CD上,且AE=CF,EF与BD相交于点O,求证:OB=OD.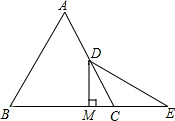 已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.
已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.