题目内容
 如图,在平面直角坐标系中,平行四边形ABCO的边OA在x轴上,O(0,0),A(3,0),B(5,1).
如图,在平面直角坐标系中,平行四边形ABCO的边OA在x轴上,O(0,0),A(3,0),B(5,1).(1)求出点C的坐标.
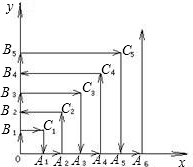
(2)在平面直角坐标系中,请你将平行四边形ABCD绕顶点O顺时针旋转3次,旋转角度分别为:90°、180°、270°,你会得到一个什么图案?
(3)若将平行四边形ABCD绕顶点O顺时针旋转120°时,求线段OB扫过的图案的面积.
考点:作图-旋转变换,平行四边形的性质,扇形面积的计算
专题:作图题
分析:(1)根据平行四边形的对边平行且相等求出OA的长度为3,然后把点B的坐标向左平移3个单位长度即可得解;
(2)分别找出点A、B、C旋转后的对应点的位置,然后顺次连接即可得到图案;
(3)先根据点B的坐标利用勾股定理求出OB的长度,再利用扇形的面积公式列式计算即可得解.
(2)分别找出点A、B、C旋转后的对应点的位置,然后顺次连接即可得到图案;
(3)先根据点B的坐标利用勾股定理求出OB的长度,再利用扇形的面积公式列式计算即可得解.
解答: 解:(1)∵O(0,0),A(3,0),
解:(1)∵O(0,0),A(3,0),
∴OA=3-0=3,
∵四边形ABCO是平行四边形,
∴OA=BC,
∵B(5,1),
5-3=2,
∴点C的坐标是(2,1);
(2)如图所示图案;
(3)∵B(5,1),
∴OB=
=
,
又∵旋转角为120°,
∴线段OB扫过的图案的面积=
=
π.
 解:(1)∵O(0,0),A(3,0),
解:(1)∵O(0,0),A(3,0),∴OA=3-0=3,
∵四边形ABCO是平行四边形,
∴OA=BC,
∵B(5,1),
5-3=2,
∴点C的坐标是(2,1);
(2)如图所示图案;
(3)∵B(5,1),
∴OB=
| 52+12 |
| 26 |
又∵旋转角为120°,
∴线段OB扫过的图案的面积=
120•π
| ||
| 360 |
| 26 |
| 3 |
点评:本题考查了利用旋转变换作图,平行四边形的性质,扇形的面积计算,以及勾股定理的应用,熟练掌握平行四边形的性质以及扇形的面积公式是求解的关键.

练习册系列答案
相关题目
化简
等于( )
| (sin28°-cos28°)2 |
| A、sin28°-cos28° |
| B、0 |
| C、cos28°-sin28° |
| D、以上都不对 |
下列等式成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列事件中,不是随机事件的是( )
| A、某射击运动员,在练习射击中,一共射击50次,其中有10次击中靶心 |
| B、小明从一副扑克牌中抽取一张,结果他抽的是大王 |
| C、从装有黑、白各3颗围棋子的袋中抽取4颗,结果有黑白两种棋子 |
| D、同时抛掷两枚质地均匀的骰子一次,结果点数之和是6 |
 )时所需要的时间.
)时所需要的时间. 如图,梯形ABCD中,AD∥BC,AB⊥AD,AD=7,BC=9.若DE⊥DC,且DE=DC,则△ADE的面积是
如图,梯形ABCD中,AD∥BC,AB⊥AD,AD=7,BC=9.若DE⊥DC,且DE=DC,则△ADE的面积是