题目内容
17.计算:(1)[(x3)2•(-x4)3]÷(-x6)3;
(2)(xm•x2n)2÷(-xm+n);
(3)(m-2n)4÷(2n-m)2;
(4)(m-n)4÷(n-m)3.
分析 (1)按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似;
(2)按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似;
(3)先化为同底数的幂再运算;
(4)先把(m-n)4化为(n-m)4再运算.
解答 解:(1)原式=(-x6•x12)÷(-x18)=(-x18)÷(-x18)=1;
(2)原式=(xm+2n)÷(-xm+n)=-xn;
(3)原式=(m-2n)4÷(m-2n)2=(m-2n)2;
(4)原式=(n-m)4÷(n-m)3=n-m.
点评 本题主要考查了整式的混合运算,熟练掌握运算法则,不同底数的幂化为相同底数的幂是解答此题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
8.|-9|的平方根等于( )
| A. | ±3 | B. | 3 | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
12.某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶6元的价格出售,如果当天卖不完,剩余的只有倒掉.店主记录了30天的日需求量(单位:瓶),整理得下表:
(1)求这30天内日需求量的众数;
(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数;
(3)以30记录的各需求量的频率作为各需求是发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.
| 日需求量 | 26 | 27 | 28 | 29 | 30 |
| 频数 | 5 | 8 | 7 | 6 | 4 |
(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数;
(3)以30记录的各需求量的频率作为各需求是发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.
9.2014年天津市全市经济运行情况显示,天津市2014年实现地区生产总值(GDP)15722.47亿元,其中15722.47用科学记数法表示为( )
| A. | 1.572247×105 | B. | 15.72247×103 | C. | 1.572247×104 | D. | 15.72247×102 |
8.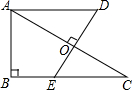 如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )
如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )
 如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )
如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )| A. | $\frac{25}{4}$ | B. | $\frac{25}{8}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
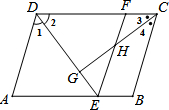 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).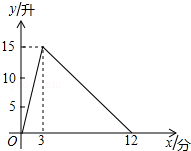 一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,时间x的取值范围为1<x<9.
一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,时间x的取值范围为1<x<9.