题目内容
1.在△ABC中,AD是角平分线,AB=24,AC=36,S△ABD=S△ADC,此题中“角平分线”这个条件的作用是角的平分线上的点到角的两边的距离相等.分析 根据角的平分线上的点到角的两边的距离相等解答即可.
解答 解:因为角平分线到角两边的距离相等,即DE=DF,
所以S△ABD=S△ADC,
利用的是角的平分线上的点到角的两边的距离相等;
故答案为:S△ADC;角的平分线上的点到角的两边的距离相等.
点评 本题考查了角平分线的性质;要熟练掌握角平分线的性质,会求三角形的面积.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
11.下列变形中不正确的是( )
| A. | 若5x+8=4x,则5x-4x=8 | B. | 若3x-1=x+3,则2x=4 | ||
| C. | 若2=x,则x=2 | D. | 若x-1=3,则x=4 |
12. 如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
 如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 60° |
6.已知a+$\frac{1}{a}$=$\sqrt{10}$,则a-$\frac{1}{a}$的值为( )
| A. | 2 | B. | 6 | C. | ±$\sqrt{6}$ | D. | ±2$\sqrt{2}$ |
13.下列式子(1)$\sqrt{6}$,(2)$\sqrt{{a}^{2}+1}$,(3)$\root{3}{9}$,(4)$\sqrt{{a}^{2}+2a+1}$,(5)$\sqrt{|{m}^{2}-1|}$中,是二次根式的是( )
| A. | (1)(2)(3)(4) | B. | (2)(3)(4)(5) | C. | (1)(2)(3)(5) | D. | (1)(2)(4)(5) |
10. 某中学举行“校园•朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行“校园•朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
(2)结合两队成绩的平均数和中位数,初中队的决赛成绩较好;
(3)已知高中代表队决赛成绩的方差为160,计算初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.(方差公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]
 某中学举行“校园•朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行“校园•朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写表格;
(2)结合两队成绩的平均数和中位数,初中队的决赛成绩较好;
(3)已知高中代表队决赛成绩的方差为160,计算初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.(方差公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]
| 平均分(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
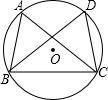 如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.
如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB. 如图,已知线段AB=4cm.
如图,已知线段AB=4cm. 如图,已知∠APN=30°,则轮船A在灯塔P的北偏东30°的方向上;轮船B在灯塔P的南偏东70°的方向上,则∠APB=80度,若轮船C在∠APB的角平分线上,则轮船C在灯塔P的北偏东70°的方向上.
如图,已知∠APN=30°,则轮船A在灯塔P的北偏东30°的方向上;轮船B在灯塔P的南偏东70°的方向上,则∠APB=80度,若轮船C在∠APB的角平分线上,则轮船C在灯塔P的北偏东70°的方向上.