��Ŀ����
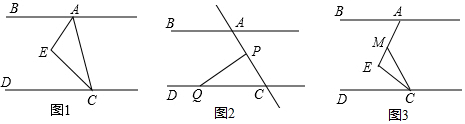
12����ͼ1��CEƽ�֡�ACD��AEƽ�֡�BAC����EAC+��ACE=90����1�����ж�AB��CD��λ�ù�ϵ��˵�����ɣ�
��2����ͼ2��PΪ�߶�AC��һ���㣬��QΪֱ��CD��һ������AB��CD��λ�ù�ϵ���ֲ��䣬����Q������CD���˶�ʱ����C���⣩��CPQ+��CQP���BAC�к�������ϵ����BAC=��PQC+��QPC������ֱ��д���𰸣�
��3����ͼ3������E=90����AB��CD��λ�ù�ϵ���ֲ��䣬�ƶ�ֱ�Ƕ���E��ʹ��MCE=��ECD����ֱ�Ƕ���E���ƶ�ʱ���ʡ�BAE���MCD�����ȷ����������ϵ����˵�����ɣ�
���� ��1���ȸ���CEƽ�֡�ACD��AEƽ�֡�BAC�ó���BAC=2��EAC����ACD=2��ACE�����ɡ�EAC+��ACE=90���֪��BAC+��ACD=180���ʿɵó����ۣ�
��2������AB��CD��֪��BAC+��ACD=180�㣬��QPC+��PQC+��PCQ=180�㣬�ʡ�BAC=��PQC+��QPC��
��3����E��EF��AB������ƽ���ߵ����ʿ�֪EF��AB��CD����BAE=��AEF����FEC=��DCE���ʡ�BAE+��ECD=90�㣬���ɡ�MCE=��ECD���ɵó����ۣ�
��� �⣺��1��AB��CD��
���ɣ���CEƽ�֡�ACD��AEƽ�֡�BAC��
���BAC=2��EAC����ACD=2��ACE��
�ߡ�EAC+��ACE=90�㣬
���BAC+��ACD=180�㣬
��AB��CD��
��2����AB��CD��
���BAC+��ACD=180�㣬
�ߡ�QPC+��PQC+��PCQ=180�㣬
���BAC=��PQC+��QPC��
�ʴ�Ϊ����BAC=��PQC+��QPC��
��3����BAE+$\frac{1}{2}$��MCD=90�㣮
��ͼ3����E��EF��AB��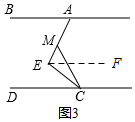
��AB��CD��
��EF��AB��CD��
���BAE=��AEF����FEC=��DCE��
�ߡ�E=90�㣬
���BAE+��ECD=90�㣬
�ߡ�MCE=��ECD��
���BAE+$\frac{1}{2}$��MCD=90�㣮
���� ���⿼����ƽ���ߵ����ʣ�������������ƽ�����ǽ�����Ĺؼ�������ʱע�⣺�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ�

| A�� | 2a-1��0 | B�� | 2a+1��0 | C�� | 2a-1��0 | D�� | 2a+1��0 |
| A�� | 5��$\sqrt{10}$ | B�� | -5��$\sqrt{10}$ | C�� | 5����$\sqrt{10}$ | D�� | -5����$\sqrt{10}$ |
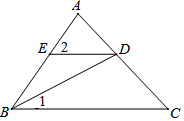 ��֪����ͼ��BDƽ�֡�ABC����1=25�㣬��2=50�㣮���ж�ED��BC��λ�ù�ϵ��˵�����ɣ�
��֪����ͼ��BDƽ�֡�ABC����1=25�㣬��2=50�㣮���ж�ED��BC��λ�ù�ϵ��˵�����ɣ�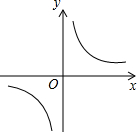 ��֪����������y=$\frac{k-2}{x}$��ͼ����ͼ����һԪ���η���x2-��2k-1��x+k2-1=0�����������ʵ������
��֪����������y=$\frac{k-2}{x}$��ͼ����ͼ����һԪ���η���x2-��2k-1��x+k2-1=0�����������ʵ������