题目内容
18.已知:关于x的一元二次方程(m-1)x2+(m-2)x-1=0(m为实数)若方程有两个不相等的实数根,求m的取值范围.分析 根据方程有两个不相等的实数根可知△>0,再由一元二次方程的定义得出m≠1,由此可得出结论.
解答 解:此方程的判别式△=(m-2)2+4(m-1)=m2,
∵方程有两个不相等的实数根,
∴m≠0.
∵m-1≠0,
∴m的取值范围是m≠0且m≠1.
点评 本题考查了根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的实数根;
②当△=0时,方程有两个相等的实数根;
③当△<0时,方程无实数根.
也考查了一元二次方程的定义.

练习册系列答案
相关题目
18.点A(3,-5)向左平移3个单位,再向上平移4个单位到点B,则点B的坐标为( )
| A. | (1,-8) | B. | (1,-2) | C. | (-7,-1) | D. | (0,-1) |
3.下列代数式是最简形式的是( )
| A. | $\frac{{{x^2}-4}}{x-2}$ | B. | $\frac{{4{x^2}+4x+1}}{2x+1}$ | C. | $\sqrt{4{x^3}}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
7.下列结论中正确的是( )
| A. | 分式$\frac{1}{x(x-1)}$有意义的条件是x≠0或x≠1 | |
| B. | 以长为3cm,5cm,7cm,10cm的四条线段中的三条线段为边,构成三角形的情况有1种 | |
| C. | -0.0000064用科学记数法表示为-6.4×10-6 | |
| D. | 等式(x2-9)0=1成立的条件是x=±3 |
8.下列各数中,是不等式2x+1≥7的解的是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
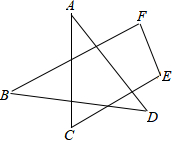 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数. BD平分∠ABC,CD平分外角∠ACG,DE∥BC交AB于E,交AC于F,线段EF与BE、CF有什么关系?
BD平分∠ABC,CD平分外角∠ACG,DE∥BC交AB于E,交AC于F,线段EF与BE、CF有什么关系?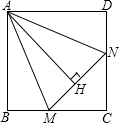 已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.
已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.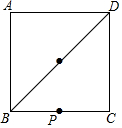 一个正方形的田地,BD所在线段种的是苹梨树,小明家在BC中点P处.他要从家出发摘苹果然后拿到位于点C处的集市上去卖,请在BD上找一点M,使得小明所走路径最短,即PM+CM最短,(要求:尺规作图,不写作法,保留作图痕迹)
一个正方形的田地,BD所在线段种的是苹梨树,小明家在BC中点P处.他要从家出发摘苹果然后拿到位于点C处的集市上去卖,请在BD上找一点M,使得小明所走路径最短,即PM+CM最短,(要求:尺规作图,不写作法,保留作图痕迹)