题目内容
16．
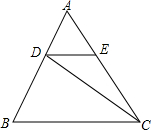如图，DE∥BC，S△ADE=2，S△DBC=12，则S△CDE=4．
分析 根据已知条件得到△ADE∽△ABC，由相似三角形的性质得到得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=$\frac{2}{s}$，于是求得$\frac{AD}{BD}$=$\frac{\sqrt{2}}{\sqrt{s}-\sqrt{2}}$，根据$\frac{{S}_{△ADC}}{{S}_{△BCD}}$=$\frac{AD}{BD}$，列方程解得s=18，于是得到结论．
解答 解：设S△ABC=s，
∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=$\frac{2}{s}$，
∴$\frac{AD}{BD}$=$\frac{\sqrt{2}}{\sqrt{s}-\sqrt{2}}$，
∴$\frac{{S}_{△ADC}}{{S}_{△BCD}}$=$\frac{AD}{BD}$，
即$\frac{s-12}{12}$=$\frac{\sqrt{2}}{\sqrt{s}-\sqrt{2}}$，
解得s=18，
∴S△CDE=S△ABC-S△ADE-S△BCD=4，
故答案为：4．
点评 本题主要考查了相似三角形的判定与性质及三角形的面积，解题的关键是利用三角形的面积之比等于相似三角形的对应边的平方比．
练习册系列答案
相关题目
6．
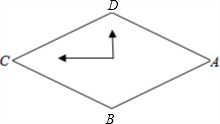某课外小组设计了一个菱形挂钟．如图，菱形的边长为12厘米，时钟的中心在菱形的交点上，∠ADC=120°，数字3，6，9，12分别在四个顶点ABCD上，则数字1的位置与D点的距离为（ ）
某课外小组设计了一个菱形挂钟．如图，菱形的边长为12厘米，时钟的中心在菱形的交点上，∠ADC=120°，数字3，6，9，12分别在四个顶点ABCD上，则数字1的位置与D点的距离为（ ）| A． | 3厘米 | B． | 4厘米 | C． | 3$\sqrt{3}$厘米 | D． | 6厘米 |
如图，△ABC中，$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$，求$\frac{OE}{OB}$的值．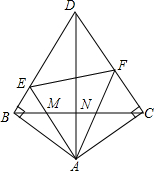
已知，如图所示四边形ABDC，DB⊥AB，CD⊥AC，AB=AC，∠EAF=∠BDC=60°，AE，AF分别交BC于点M，N，下列结论：
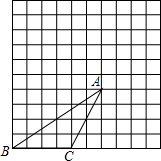在如图所示10×10的方格中，有一个格点△ABC，请在图中画出两个格点△A1B1C1 和△A2B2C2，使△ABC∽△A1B1C1∽△A2B2C2（相似比不为1，且△A1B1C1为放大的三角形，△A2B2C2为缩小的三角形）．
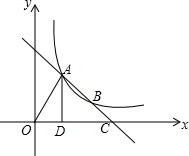如图，直线AB交双曲线y=$\frac{k}{x}$于A，B，交x轴于点C，过A作AD⊥x轴于D，且OD=$\frac{1}{3}$OC，S△OAC=12．则k的值为8．
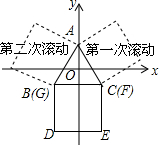如图，边长为2的等边三角形ABC的重心与坐标原点重合，边BC与x轴平行，正方形DEFG的一边GF与BC重合，将正方形DEFG绕等边三角形ABC按逆时针方向做如图所示的无滑动滚动，做完第2015次滚动后，点D的坐标为（-1，-$\frac{\sqrt{3}}{3}$）．