题目内容
2.二次函数y=-x2+2x+m的图象与x轴交于A、B两点(B在A右侧),顶点为C,且A、B两点间的距离等于点C到y轴的距离的2倍.(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
分析 (1)先把m当作已知条件求出点C的坐标及抛物线与x轴的交点坐标,再由A、B两点间的距离等于点C到y轴的距离的2倍即可得出m的值,进而得出结论;
(2)根据(1)中m的值可得出B、C两点的坐标,利用待定系数法可得出直线BC的解析式;
(3)设点P(1,n),过点P作PD⊥BC,根据(2)中直线BC的解析式可知∠OBC的度数,故可用n表示出PC的长,进而得出结论.
解答 解:(1)∵二次函数的解析式为y=-x2+2x+m,
∴顶点为C(1,m+1),与x轴交于A(1-$\sqrt{1+m}$,0)、B(1+$\sqrt{1+m}$,0).
∵A、B两点间的距离等于点C到y轴的距离的2倍,
∴(1-$\sqrt{1+m}$)-(1+$\sqrt{1+m}$)=2,解得m=0,
∴抛物线的解析式为:y=-x2+2x;
(2)∵由(1)知,m=0,
∴B(2,0),C(1,1).
设直线BC的解析式为y=kx+b(k≠0),则$\left\{\begin{array}{l}2k+b=0\\ k+b=1\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=2\end{array}\right.$,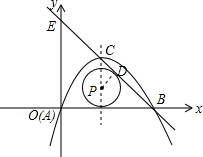
∴直线BC的解析式为:y=-x+2;
(3)如图,设点P(1,n),过点P作PD⊥BC,
∵由(2)知直线BC的解析式为y=-x+2,
∴∠AEB=45°.
∵∴PC=$\sqrt{2}$n,
∴1-n=$\sqrt{2}$n,
∴n=$\sqrt{2}$-1,
∴点P(1,$\sqrt{2}$-1).
点评 本题考查的是二次函数综合题,涉及到二次函数与坐标轴的交点问题及用待定系数法求一次函数的解析式,切线的性质等知识,根据题意画出图形,利用数形结合求解是解答此题的关键.

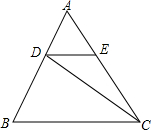 如图,DE∥BC,S△ADE=2,S△DBC=12,则S△CDE=4.
如图,DE∥BC,S△ADE=2,S△DBC=12,则S△CDE=4. (1)如图所示,边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成矩形,这样就能验证分解因式的一个公式,这个公式是什么?并写出验证过程.
(1)如图所示,边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成矩形,这样就能验证分解因式的一个公式,这个公式是什么?并写出验证过程.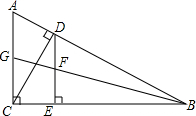 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.