题目内容
5.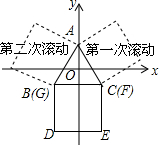 如图,边长为2的等边三角形ABC的重心与坐标原点重合,边BC与x轴平行,正方形DEFG的一边GF与BC重合,将正方形DEFG绕等边三角形ABC按逆时针方向做如图所示的无滑动滚动,做完第2015次滚动后,点D的坐标为(-1,-$\frac{\sqrt{3}}{3}$).
如图,边长为2的等边三角形ABC的重心与坐标原点重合,边BC与x轴平行,正方形DEFG的一边GF与BC重合,将正方形DEFG绕等边三角形ABC按逆时针方向做如图所示的无滑动滚动,做完第2015次滚动后,点D的坐标为(-1,-$\frac{\sqrt{3}}{3}$).
分析 2015÷3=671…2,所以第2015次滚动后,正方形DEFG在第二次滚动的位置,D与B重合,求出点B的坐标即可.
解答 解:∵等边△ABC边长为2,O为重心,
∴B(-1,-$\frac{\sqrt{3}}{3}$),
将正方形DEFG绕等边三角形ABC按逆时针方向做如图所示的无滑动滚动,做完第2015次滚动,
∵2015÷3=671…2,
∴第2015次滚动后,正方形DEFG在第二次滚动的位置,D与B重合,
∴D(-1,-$\frac{\sqrt{3}}{3}$).
故答案为:(-1,-$\frac{\sqrt{3}}{3}$).
点评 本题主要考查了点的坐标,根据重心的性质求出点B的坐标,发现第2015次滚动后,正方形DEFG在第二次滚动的位置D与B重合,是解决问题的关键.

练习册系列答案
相关题目

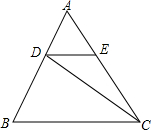 如图,DE∥BC,S△ADE=2,S△DBC=12,则S△CDE=4.
如图,DE∥BC,S△ADE=2,S△DBC=12,则S△CDE=4. (1)如图所示,边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成矩形,这样就能验证分解因式的一个公式,这个公式是什么?并写出验证过程.
(1)如图所示,边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成矩形,这样就能验证分解因式的一个公式,这个公式是什么?并写出验证过程.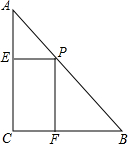 已知a、b为直角三角形两直角边,且a、b为一元二次方程:x2-(2k+1)x+k2+k+$\frac{1}{4}$=0的两根.
已知a、b为直角三角形两直角边,且a、b为一元二次方程:x2-(2k+1)x+k2+k+$\frac{1}{4}$=0的两根.