题目内容
6.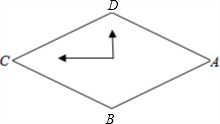 某课外小组设计了一个菱形挂钟.如图,菱形的边长为12厘米,时钟的中心在菱形的交点上,∠ADC=120°,数字3,6,9,12分别在四个顶点ABCD上,则数字1的位置与D点的距离为( )
某课外小组设计了一个菱形挂钟.如图,菱形的边长为12厘米,时钟的中心在菱形的交点上,∠ADC=120°,数字3,6,9,12分别在四个顶点ABCD上,则数字1的位置与D点的距离为( )| A. | 3厘米 | B. | 4厘米 | C. | 3$\sqrt{3}$厘米 | D. | 6厘米 |
分析 设时钟的中心为O点,数字1所在的位置是E点,连结AC、OD、OE,根据菱形的性质得出∠ODC=∠ODE=$\frac{1}{2}$∠ADC=60°,OD⊥AC,∠DOE=$\frac{1}{3}$∠AOD=30°.解Rt△ODC求出OD=$\frac{1}{2}$CD=6cm,解Rt△ODE,求出DE=$\frac{1}{2}$OD=3cm.
解答 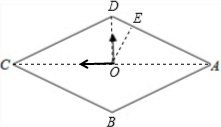 解:设时钟的中心为O点,数字1所在的位置是E点,连结AC、OD、OE.
解:设时钟的中心为O点,数字1所在的位置是E点,连结AC、OD、OE.
∵四边形ABCD是菱形,
∴∠ODC=∠ODE=$\frac{1}{2}$∠ADC=60°,OD⊥AC,∠DOE=$\frac{1}{3}$∠AOD=30°.
∵在Rt△ODC中,∠COD=90°,∠OCD=30°,
∴OD=$\frac{1}{2}$CD=6cm.
∵在Rt△ODE中,∠OED=180°-∠DOE-∠ODE=180°-30°-60°=90°,∠DOE=30°,
∴DE=$\frac{1}{2}$OD=3cm.
故选A.
点评 本题考查了菱形的性质,含30°角的直角三角形的性质,求出∠OED=90°是解题的关键.

练习册系列答案
相关题目
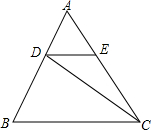 如图,DE∥BC,S△ADE=2,S△DBC=12,则S△CDE=4.
如图,DE∥BC,S△ADE=2,S△DBC=12,则S△CDE=4.