题目内容
写出二元一次方程2x-y=4的一个整数解 .
考点:解二元一次方程
专题:开放型
分析:把x看做已知数求出y,即可确定出整数解.
解答:
解:方程2x-y=4,
解得:y=2x-4,
当x=1时,y=-2,
则方程的一个整数解为
,
故答案为:
解得:y=2x-4,
当x=1时,y=-2,
则方程的一个整数解为
|
故答案为:
|
点评:此题考查了解二元一次方程,解题的关键是将一个未知数看做已知数求出另一个未知数.

练习册系列答案
相关题目
将方程x2-6x+5=0化成(x+m)2=n的形式,则m,n分别是( )
| A、m=-3,n=4 |
| B、m=3,n=-4 |
| C、m=-1,n=-5 |
| D、m=-5,n=-1 |
下列各式能用平方差公式分解因式的个数是( )
(1)x2+y2;(2)-x2+y2;(3)x2-y2;(4)-x2-y2.
(1)x2+y2;(2)-x2+y2;(3)x2-y2;(4)-x2-y2.
| A、1个 | B、2个 | C、3个 | D、4个 |
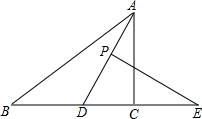 在△ABC中,AD平分角∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
在△ABC中,AD平分角∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.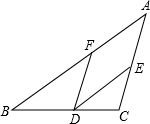 请将下面证明中的每一步的理由填在相应的括号内:
请将下面证明中的每一步的理由填在相应的括号内: