Question

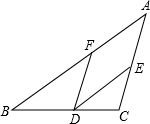
请将下面证明中的每一步的理由填在相应的括号内：
已知：如图，D，E，F分别是BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠AFD=∠EDC+∠C．
证明：∵DE∥BA，DF∥CA

 

∴∠AED与∠A互补，∠AFD与∠A互补

 

∴∠AED=∠AFD

 

∵∠AED=∠EDC+∠C

 

∴∠AFD=∠EDC+∠C

 

．

Answer 1

考点：平行线的性质

专题：推理填空题

分析：先根据平行线的性质得出∠AED与∠A互补，∠AFD与∠A互补，故∠AED=∠AFD，再由三角形外角的性质得出∠AED=∠EDC+∠C，由此可得出结论．

解答： 证明：∵DE∥BA，DF∥CA，
∴∠AED与∠A互补，∠AFD与∠A互补，
∴∠AED=∠AFD．
∵∠AED=∠EDC+∠C，
∴∠AFD=∠EDC+∠C．
故答案为：已知，两直线平行，同旁内角互补，等量代换，三角形外角的性质，等量代换．

点评：本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．