题目内容
 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,AD与EF交于点G,请探索EF与AD的关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,AD与EF交于点G,请探索EF与AD的关系,并说明理由.考点:角平分线的性质,线段垂直平分线的性质
专题:
分析:根据条件可得DE=DF,且可得到AE=AF,可得到AD垂直平分EF.
解答:解:AD垂直平分EF,理由如下:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴∠DEF=∠DFE,
又∠AED=∠AFD=90°,
∴∠AEF=∠AFE,
∴AE=AF,
∴点D,点A在EF的垂直平分线上,
∴AD是线段EF的垂直平分线.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴∠DEF=∠DFE,
又∠AED=∠AFD=90°,
∴∠AEF=∠AFE,
∴AE=AF,
∴点D,点A在EF的垂直平分线上,
∴AD是线段EF的垂直平分线.
点评:本题主要考查角平分线的性质和线段垂直平分线的判定,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
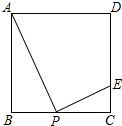 如图,在正方形ABCD中,点E在CD上,CE=
如图,在正方形ABCD中,点E在CD上,CE= 如图,BC是⊙O的直径,点A是
如图,BC是⊙O的直径,点A是