题目内容
20.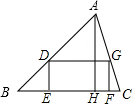 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.(1)求证:AM•BC=AH•DG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
分析 (1)根据矩形的对边平行得到DG∥EF,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”得到△ADG∽△ABC,再根据相似三角形对应高的比等于相似比得到$\frac{AM}{AH}$=$\frac{DG}{BC}$,然后利用比例的基本性质即可证明AM•BC=AH•DG;
(2)当加工成的矩形零件DEFG的面积等于25cm2时,设宽DE的长度为xcm,则AM=(8-x)cm,DG=$\frac{25}{x}$cm.根据(1)中结论AM•BC=AH•DG,列出方程(8-x)×10=8×$\frac{25}{x}$,整理得x2-8x+20=0,进而求解即可.
解答  (1)证明:∵四边形DEFG为矩形,
(1)证明:∵四边形DEFG为矩形,
∴DG∥EF,
∴△ADG∽△ABC,
∴$\frac{AM}{AH}$=$\frac{DG}{BC}$,
∴AM•BC=AH•DG;
(2)解:加工成的矩形零件DEFG的面积不能等于25cm2,理由如下:
当加工成的矩形零件DEFG的面积等于25cm2时,设宽DE的长度为xcm,则AM=(8-x)cm,DG=$\frac{25}{x}$cm.
∵高线AH长8cm,底边BC长10cm,AM•BC=AH•DG,
∴(8-x)×10=8×$\frac{25}{x}$,
整理得x2-8x+20=0,
∵△=64-4×20=-16<0,
∴x无实数根,
故加工成的矩形零件DEFG的面积不能等于25cm2.
点评 此题考查了相似三角形的应用,矩形的性质,一元二次方程的应用,解题的关键是利用相似三角形对应边的比等于其对应高的比,得出$\frac{AM}{AH}$=$\frac{DG}{BC}$.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5.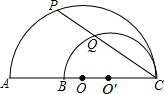 如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
 如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )| A. | 5cm | B. | 5$\sqrt{3}$cm | C. | 6cm | D. | 8cm |
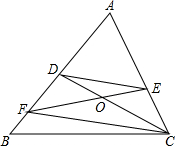 如图,在△ABC中,∠ACD=∠B,将△ACD绕A点旋转,点D落在点E处,点C落在点F处,CD,EF交于O点,连接DE,FC,找出其中相似三角形.
如图,在△ABC中,∠ACD=∠B,将△ACD绕A点旋转,点D落在点E处,点C落在点F处,CD,EF交于O点,连接DE,FC,找出其中相似三角形.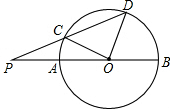 如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数.
如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数. 画出以下几何体的三视图.
画出以下几何体的三视图. 如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求:
如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求: