题目内容
9.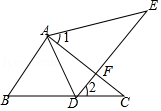 如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.(1)求证:AB=AD;
(2)若∠1=60°,判断△ABD的形状,并说明理由.
分析 (1)根据三角形内角和定理得到∠E=∠C,再根据AC=AE,∠C=∠E,BC=DE,判定△ABC≌△ADE,即可得到AB=AD.
(2)根据等腰三角形的性质以及全等三角形的性质,可得∠ADB=∠ADE,进而得出$∠ADB=\frac{1}{2}∠BDE={60°}$,可得△ABD是等边三角形.
解答 解:(1)∵∠1+∠AFE+∠E=180°,
∴∠E=180°-∠1-∠AFE,
∵∠2+∠CFD+∠C=180°,
∴∠C=180°-∠2-∠CFD,
∵∠1=∠2,∠AFE=∠CFD,
∴∠E=∠C,
∵AC=AE,∠C=∠E,BC=DE,
∴△ABC≌△ADE,
∴AB=AD.
(2)△ABD是等边三角形.理由:
∵∠1=∠2=60°,
∴∠BDE=180°-∠2=120°,
∵AB=AD,
∴∠B=∠ADB,
∵△ABC≌△ADE,
∴∠B=∠ADE,
∴∠ADB=∠ADE,
∴$∠ADB=\frac{1}{2}∠BDE={60°}$,
∴△ABD是等边三角形.
点评 本题考查全等三角形的判定和性质、三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题.

练习册系列答案
相关题目
20.在△ABC中,∠C=90°,tanA=1,那么cosB等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
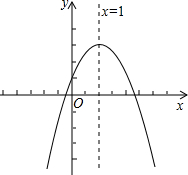 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论: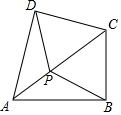 如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,P为对角线AC上任一点,求证:PB=PD.
如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,P为对角线AC上任一点,求证:PB=PD.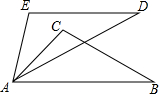 如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.
如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.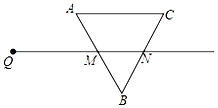 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2 cm,QM=4 cm.动点P从Q出发,沿射线QN以每秒1 cm的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径的⊙P与△ABC的AB边相切(切点在边上),则t值为2或6秒.
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2 cm,QM=4 cm.动点P从Q出发,沿射线QN以每秒1 cm的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径的⊙P与△ABC的AB边相切(切点在边上),则t值为2或6秒.