题目内容
16．
如图，在四边形ABCD中，∠B+∠D=180°，∠DCE是四边形ABCD的一个外角，∠DCE与∠A相等吗？为什么？
分析 先根据四边形内角和为360°得出∠A+∠BCD=180°，再由邻补角定义得出∠DCE+∠BCD=180°，然后根据同角的补角相等即可得到∠DCE=∠A．
解答 解：∵在四边形ABCD中内角和为360°，
∴∠A+∠B+∠BCD+∠D=360°，
又∵∠B+∠D=180°，
∴∠A+∠BCD=180°，
又∵∠DCE+∠BCD=180°，
∴∠DCE=∠A．
点评 题考查了多边形内角与外角，四边形内角和定理，补角的性质，解决本题的关键是根据四边形内角和为360°得出∠A+∠BCD=180°．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
6．下列式子中，正确的是（ ）
| A． | （a+1）2=a2+1 | B． | a2+a3=a5 | C． | a6÷a2=a3（a≠0） | D． | （-a2b）3=-a6b3 |
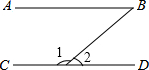如图，AB∥CD，∠B+∠2=160°，则∠1=100°．