题目内容
1.在菱形ABCD中,对角线AC、BD相交于点O.如果AC=6,BD=8,那么菱形的周长是20.分析 由菱形的性质得出AB=BC=CD=AD,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD=4,AC⊥BD,根据勾股定理求出AB,菱形的周长=4AB,即可得出结果.
解答 解:如图所示: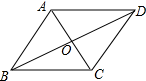 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD=4,AC⊥BD,
∴∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴菱形的周长=4AB=20;
故答案为:20.
点评 本题考查了菱形的性质、勾股定理的运用;熟练掌握菱形的性质,运用勾股定理求出边长是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.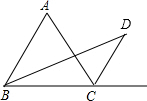 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )
如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )
 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )
如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )| A. | 15° | B. | 25° | C. | 30° | D. | 30° |
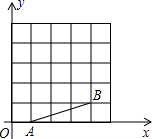 如图,在平面直角坐标系中,A,B,C均在边长为1的正方形网格格点上,反比例函数y=$\frac{k}{x}$(x>0)经过B,C两点.
如图,在平面直角坐标系中,A,B,C均在边长为1的正方形网格格点上,反比例函数y=$\frac{k}{x}$(x>0)经过B,C两点. 如图,在四边形ABCD中,∠B+∠D=180°,∠DCE是四边形ABCD的一个外角,∠DCE与∠A相等吗?为什么?
如图,在四边形ABCD中,∠B+∠D=180°,∠DCE是四边形ABCD的一个外角,∠DCE与∠A相等吗?为什么?