题目内容
13.先化简下列代数式,再求当x=$\sqrt{3}$-5时,下列代数式的值.$\frac{1}{(x-1)(x+1)}$+$\frac{1}{(x+1)(x+3)}$+…+$\frac{1}{(x+9)(x+11)}$.
分析 原式利用拆项法变形后,抵消合并得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{1}{2}$($\frac{1}{x-1}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+3}$+…+$\frac{1}{x+9}$-$\frac{1}{x+11}$)=$\frac{1}{2}$($\frac{1}{x-1}$-$\frac{1}{x+11}$)=$\frac{1}{2}$•$\frac{x+11-x+1}{(x-1)(x+11)}$=$\frac{6}{(x-1)(x+11)}$,
当x=$\sqrt{3}$-5时,原式=$\frac{6}{(\sqrt{3}-6)(\sqrt{3}+6)}$=-$\frac{2}{9}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
18.下列各数不属于分数的是( )
| A. | -0.314 | B. | 3.$\stackrel{•}{1}$$\stackrel{•}{4}$ | C. | 3.14… | D. | -$\frac{14}{3}$ |
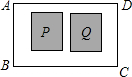 要对一块长60米、宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{4}$,求P、Q两块绿地周围的硬化路面的宽,设硬化路面的宽为x米.
要对一块长60米、宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{4}$,求P、Q两块绿地周围的硬化路面的宽,设硬化路面的宽为x米.