题目内容
 如图,⊙O的弦AB垂直于弦CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到AB的距离是
如图,⊙O的弦AB垂直于弦CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到AB的距离是考点:垂径定理,勾股定理
专题:
分析:作OM⊥AB于M,ON⊥CD于N.则四边形OMEN是矩形,则O到CD的距离ON=EM,根据垂径定理求得EM的长,再由AB=CD可知OM=EM,由此可得出结论.
解答: 解:作OM⊥AB于M,ON⊥CD于N.则四边形OMEN是矩形.
解:作OM⊥AB于M,ON⊥CD于N.则四边形OMEN是矩形.
∵OM⊥AB于M,
∴AM=MB=
AB=
(AE+BE)=
(3+7)=5.
∴EM=AM-AE=5-3=2.
∴ON=EM=2.
∵AB=CD,
∴OM=EM=2.
故答案是:2.
 解:作OM⊥AB于M,ON⊥CD于N.则四边形OMEN是矩形.
解:作OM⊥AB于M,ON⊥CD于N.则四边形OMEN是矩形.∵OM⊥AB于M,
∴AM=MB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EM=AM-AE=5-3=2.
∴ON=EM=2.
∵AB=CD,
∴OM=EM=2.
故答案是:2.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、必然发生的事件发生的概率为1 |
| B、不确定事件发生的概率为0 |
| C、随机事件发生的概率大于0且小于1 |
| D、不可能发生的事件发生的概率为0 |
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是 如图所示,△ACB中,∠ACB=90°,CD⊥AB于D,则下列结论正确的有( )
如图所示,△ACB中,∠ACB=90°,CD⊥AB于D,则下列结论正确的有( )①BC>CD;②AC>AD;③AB>AC;④BC>AD.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图是由3块面积相同的瓷砖镶嵌而成的长方形地面示意图,一只小鸟随机落在阴影部分的概率为( )
如图是由3块面积相同的瓷砖镶嵌而成的长方形地面示意图,一只小鸟随机落在阴影部分的概率为( )A、
| ||
B、
| ||
C、
| ||
| D、1 |

 如图,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图,直线y=2x+2与x轴交于点A,与y轴交于点B.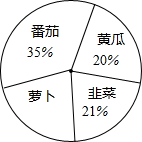 阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图.
阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图.